--->
12 задач
<---
Источники
ограничение по времени на тест
0.1 second;
ограничение по памяти на тест
64 megabytes
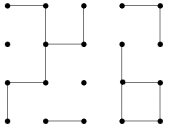
Печатной схемой называется плоская поверхность содержащей узлы и перемычки, соединяющие пары узлов. Мы будем рассматривать печатные схемы специального вида, где все узлы расположены в узлах прямоугольной сетки, а перемычки (вертикальные или горизонтальные) соединяют пары соседних узлов. Печатная схема называется связной, если любые два узла соединены друг с другом последовательностью перемычек. На вход дается печатная схема, где некоторые соседние узлы уже соединены перемычками. К ней необходимо добавить некоторое количество перемычек таким образом, чтобы схема стала связной. Стоимость вертикальной перемычки – 1, а горизонтальной – 2.
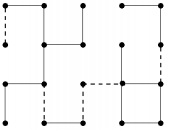Ваша программа должна по начальной печатной схеме определить количество добавляемых перемычек, минимальную стоимость такого добавления, а также вывести сами добавляемые перемычки.
Входные данные
Первая строка входного файла содержит два натуральных числа \(N\) и \(M\) – количество строк (\(1 \leq N \leq 100\)) и количество столбцов (\(1 \leq M \leq 100\)) соответственно. Каждый узел определяется своими координатами, нумерация начинается с верхнего левого угла (координаты (\(1\), \(1\))). Далее дается описание решетки в виде \(N\) строк по \(M\) чисел. Каждое число обозначает связь узла (\(i\), \(j\)) с узлами (\(i+1\), \(j\)) и (\(i\), \(j+1\)) в следующем формате: \(0\) – узел (\(i\), \(j\)) не соединен ни с одним из узлов (\(i+1\), \(j\)) и (\(i\), \(j+1\)). \(1\) – узел (\(i\), \(j\)) соединен только с узлом (\(i+1\), \(j\)) \(2\) – узел (\(i\), \(j\)) соединен только с узлом (\(i\), \(j+1\)) \(3\) – узел (\(i\), \(j\)) соединен и с узлом (\(i+1\), \(j\)), и с узлом (\(i\), \(j+1\)).
Выходные данные
Первая строка должна содержать два числа \(K\) и \(V\) – количество добавленных перемычек и стоимость добавления соответственно. Каждая из следующих \(K\) строк должна содержать описание добавленной перемычки в формате \(i\), \(j\), \(d\), где (\(i\), \(j\)) – координаты начального узла, а \(d\) может принимать значения \(1\) или \(2\). \(d = 1\) обозначает, что соединены узлы (\(i\), \(j\)) и (\(i+1\), \(j\)), \(d = 2\) – узлы (\(i\), \(j\)) и (\(i\), \(j+1\)). Если решений несколько – выведите любое из них.
Примеры
Входные данные
4 5 2 1 1 2 1 0 3 0 1 0 3 0 0 3 1 0 2 0 2 0
Выходные данные
5 6 1 1 1 2 3 1 3 3 1 4 3 2 2 5 1
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Напишите программу, которая будет либо находить вес ОДМВ (остовного дерева минимального веса) неориентированного взвешенного графа без петель с положительными длинами ребер, либо устанавливать, что введённый граф несвязный.
Входные данные
Первая строка входных данных содержит два числа N и M, разделенные пробелом — количество вершин и количество ребер графа. Далее следуют M строк, каждая из которых содержит по три целых числа, разделенные пробелами. Первые два из них разные, в пределах от 0 до N–1 каждое, и обозначают концы соответствующего ребра, третье — в пределах от 1 до 1000000000 и обозначает длину этого ребра. Гарантировано, что все ребра имеют различные длины. Количество вершин графа не превышает 80000, количество рёбер — 100000.
Выходные данные
Выведите на стандартный выход (экран) либо единственное число — сумму длин рёбер остовного дерева минимального веса (если граф связный), либо единственную фразу «NON-CONNECTED» (без кавычек, через дефис) если граф не связный.
Примечание
При указанных ограничениях на длины и количество ребер возможно переполнение типа int, используйте long long.
Указания.
Алгоритму Краскала, в отличие от предыдущих графовых задач, совершенно не нужно, чтобы граф был представлен списками смежности. Зато нужно сортировать ребра по длине. Разрешается самому написать сортировки (со сложностью O(N logN), иначе программа окажется не достаточно эффективной). Но рекомендуется заставить работать стандартный алгоритм sort. Для него нужно подключить заголовочный файл algorithm и указать, каким образом сравнивать структуры, представляющие ребра. Для этого можно перегрузить (overload) операцию сравнения operator < для типа, представляющего ребро (подробнее см. в книгах, help-е, а также в указаниях к задаче «Алгоритм Дейкстры за M logN»).
Примеры
Входные данные
5 7 1 2 5 1 3 2 2 3 4 2 4 3 3 4 6 0 3 20 0 4 10
Выходные данные
19
Выбрано
:
|