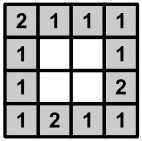
Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.

В офисе, где работает программист Петр, установили кондиционер нового типа. Этот кондиционер отличается особой простотой в управлении. У кондиционера есть всего лишь два управляемых параметра: желаемая температура и режим работы.

Кондиционер может работать в следующих четырех режимах:

• «freeze» — охлаждение. В этом режиме кондиционер может только уменьшать температуру. Если температура в комнате и так не больше желаемой, то он выключается.
• «heat» — нагрев. В этом режиме кондиционер может только увеличивать температуру. Если температура в комнате и так не меньше желаемой, то он выключается.
• «auto» — автоматический режим. В этом режиме кондиционер может как увеличивать, так и уменьшать температуру в комнате до желаемой.
• «fan» — вентиляция. В этом режиме кондиционер осуществляет только вентиляцию воздуха и не изменяет температуру в комнате.

Кондиционер достаточно мощный, поэтому при настройке на правильный режим работы он за час доводит температуру в комнате до желаемой.

Требуется написать программу, которая по заданной температуре в комнате t_room, установленным на кондиционере желаемой температуре t_cond и режиму работы определяет температуру, которая установится в комнате через час.

Всем известно, что в 2012 году прошла Летняя Олимпиада в Лондоне, однако не каждый знаком с историей крупнейших спортивных соревнований. Традиция игр зародилась в Древней Греции, но была забыта по завершении античной эпохи и вновь появилась лишь в конце XIX века благодаря французскому общественному деятелю Пьеру де Кубертену.

С 1896 года вновь проводятся летние Олимпийские игры, а с 1924 — зимние, причём оба вида соревнований проходят раз в четыре года. Первое время зимняя и летняя Олимпиады проводились в один и тот же год, но в конце XX века Международный олимпийский комитет принял решение установить между разными видами Игр двухгодичный перерыв. Таким образом, 1992 год был в последний раз отмечен проведением одновременно летних и зимних Олимпийских игр, в 1994 проводились только зимние, в 1996 — летние, и с тех пор они продолжают чередоваться.

Известно также, что в 1916, 1940 и 1944 годах Олимпийские игры были отменены по причине Первой и Второй мировых войн, а в 1906 году проводилась внеочередная Олимпиада.

Требуется написать программу, которая по заданному году определит, проводились ли в этом году Олимпийские игры и были ли они летними или зимними.

Юный математик Матвей интересуется теорией вероятностей, и по этой причине у него всегда есть с собой несколько стандартных шестигранных игральных кубиков. Стандартный шестигранный кубик имеет три противолежащих пары граней, которые размечены таким образом, что напротив грани с числом 1 находится грань с числом 6, напротив грани с числом 2 — грань с числом 5 и напротив грани с числом 3 — грань с числом 4.

Анализируя различные игры с шестигранными кубиками, Матвей придумал новую игру. В эту игру играют два игрока, и проходит она следующим образом: первый игрок бросает один или несколько стандартных кубиков (количество кубиков он определяет сам). После этого первому игроку начисляется количество очков, равное сумме чисел, оказавшихся на верхних гранях всех кубиков, а второму игроку — сумма чисел, оказавшихся на нижних гранях этих кубиков. Побеждает тот, кто набрал больше очков.

Например, если был брошен один кубик, и на верхней его грани выпало число два, то первый игрок получает два очка, а второй — пять. В свою очередь, если было брошено два кубика и на их верхних гранях выпало по единице, то первый игрок получает также два очка, а второй игрок – двенадцать очков, так как на нижних гранях этих кубиков оказались шестерки.

Матвей рассказал об этой игре своему другу, юному информатику Фоме, и они начали играть в неё через Интернет. Поскольку Фома не видит результат броска и не знает, сколько кубиков бросает Матвей как первый игрок, то о набранных каждым игроком очках он узнает только от Матвея. Чтобы проверить достоверность этой информации, Фома решил узнать, какое минимальное и максимальное количество очков мог получить он, как второй игрок, если известно, сколько очков набрал Матвей.

Требуется написать программу, которая по количеству очков, которые набрал первый игрок после броска, определяет наименьшее и наибольшее количество очков, которые может получить второй игрок за этот бросок.