Король Полигонии Трианг IV помешан на реформах. Чтобы войти в мировую историю, он решил провести территориальную реформу в своей стране. Страна Полигония имеет форму простого многоугольника, то есть ее граница не имеет самопересечений и самокасаний. В Полигонии большую роль играют внутренние диагонали — отрезки, соединяющие вершины государственной границы и полностью проходящие по территории страны, не касаясь границы. При этом форма Полигонии такова, что никакие две внутренние диагонали не лежат на одной прямой.
Вместо традиционного деления государства на административные округа король Трианг IV решил разделить свою страну на административные треугольники внутренними диагоналями. Для сокращения управляющего аппарата король повелел подготовить такой план деления страны, в котором количество административных треугольников будет минимальным.
Требуется написать программу, выполняющую деление Полигонии внутренними диагоналями на минимально возможное число административных треугольников.
Формат входных данных
В первой строке входных данных задается число N (3 ≤ N ≤ 20) — количество вершин многоугольника, образующего границу Полигонии. В следующих N строках находятся по 2 целых числа, по абсолютной величине не превосходящих 10 000 — координаты вершин в порядке обхода многоугольника против часовой стрелки. Гарантируется, что никакие три последовательные вершины многоугольника не лежат на одной прямой, и он не имеет самопересечений и самокасаний. Также гарантируется, что никакие две диагонали, содержащиеся внутри многоугольника, не лежат на одной прямой.
Формат выходных данных
В первую строку выведите наименьшее количество административных треугольников, на которое можно разбить Полигонию.
Во вторую строку выведите количество различных внутренних диагоналей K, с помощью которых можно произвести данное разбиение.
В каждую из следующих K строк выведите 4 целых числа — координаты начала и конца соответствующей диагонали разбиения, полностью лежащей внутри многоугольника и не проходящей по его границе.
Если искомых разбиений несколько, выведите любое из них.
Примеры
|
Входные данные |
Выходные данные |
Рисунок к тесту |
|
4 |
2 |
 |
|
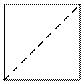10 |
4 |
 |
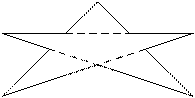На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
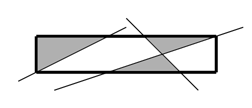
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала на вход программы поступают два положительных числа X и Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее вводится целое число N — количество разрезов (1≤N≤200). Затем описываются сами разрезы. Каждый разрез делался вдоль некоторой прямой. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все входные данные (кроме N) – вещественные числа, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число — количество частей исходного прямоугольника, имеющих треугольную форму.
Система оценки
1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤50.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4
При игре в лапту одна команда ловит мяч и пытается осалить им бегущего. Игрок другой команды должен, перед тем как бежать, ударить мяч в поле. Известно, на какое максимальное расстояние он может ударить, а также скорости и начальные координаты игроков другой команды. Требуется выбрать направление и силу удара так, чтобы минимальное время, которое потребуется другой команде, чтобы поднять мяч с земли, было наибольшим. (Пока мяч летит, игроки стоят на местах.)
В первой строке входных данных содержатся два числа: D — максимальное расстояние удара и N — количество соперников на поле (D и N натуральные числа, D ≤ 1000, N ≤ 200). В следующих N строках задается по три числа – начальные координаты xi и yi и максимальная скорость vi соответствующего игрока (скорости и координаты — целые числа, –1000 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000, 0 < vi ≤ 1000), никакие два игрока не находятся изначально в одной точке. Игрок, бьющий мяч, находится в точке с координатами (0,0). Мяч выбивается в точку с неотрицательной ординатой (y ≥ 0).
Выведите сначала время, которое потребуется игрокам, чтобы добежать до мяча, а затем координаты точки, в которую нужно выбить мяч. Если таких точек несколько, выведите координаты любой из них. Время и координаты нужно вывести с точностью 10–3.
Оценка задачи
1 балл получат программы, которые верно работают, когда в поле не более двух соперников.
10 2 1 1 1 -1 1 1
9.05539 0.00000 10.00000
Два числа – координаты точки, лежащей вне начала координат.
Одно число – величина её полярного угла (то есть угла от положительного направления оси Ох до луча с началом в точке (0,0), содержащего данную точку, против часовой стрелки).
Четыре числа – координаты двух невырожденных (т.е. ненулевых) векторов.
Одно число – величина угла \(\alpha\) между векторами (\(0\le\alpha\le\pi\)) с точностью до пятого знака после запятой.
2 1 1 2
0.64350
-2 1 -1 2
0.64350