Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
Есть две системы координат - первая и вторая. Вторая система устроена так, что ее центр в первой системе имеет координаты (A,B). Ее оси параллельны осям первой системы. При этом точка, которая во второй системе имеет координаты (1,0) в первой имеет координаты (C,B), а точка, имеющая во второй координаты (0,1) - координаты (A,D).
Дана точка, которая в первой системе имеет координаты X1,Y1.
Какие координаты она будет иметь во второй системе?
Какие координаты будет иметь точка в первой системе, если ее координаты во второй - X2, Y2?
Даны вещественные числа A, B, C, D, X1, Y1, X2, Y2.
Выведите координаты первой точки во второй системе и координаты второй точки - в первой. Все числа должны быть выведены не менее, чем с 3 знаками после десятичной точки.
1 2 5 3 0 0 0 0
-2.50000000000000E-0001 -2.00000000000000E+0000 1.00000000000000E+0000 2.00000000000000E+0000
K членов Жюри Десятой Всероссийской олимпиады школьников по информатике решили отметить столь круглую годовщину в одном из лучших ресторанов на Невском проспекте. На десерт вниманию Жюри предложили торт, имеющий форму прямоугольной призмы с выпуклым N-угольником в основании. Жюри вооружается десертными ножами и собирается справедливо разделить торт на K частей равного объема. Ножами можно проводить прямые вертикальные разрезы от одной границы торта до другой; различные разрезы могут иметь общие точки лишь в своих концевых вершинах.
Напишите программу, помогающую членам Жюри построить требуемые K-1 разрезов.
В первой строке входных данных содержатся два целых числа K и N (1 <= K, N <= 50). Далее следуют N пар вещественных чисел - координаты последовательно расположенных вершин N-угольника.
Каждый из K-1 разрезов в выходных данных должен быть представлен четверкой вещественных чисел с не менее чем 10 знаками после запятой - координатами концов соответствующего разреза. Все числа должны быть разделены пробелами и/или символами перевода строки.
2 3 1 0 0 0 0 1
1.0000000000E+00 0.0000000000E+00 0.0000000000E+00 5.0000000000E-01
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
В первой строке содержится N (3≤N≤1000) - число вершин многоугольника. В последующих N строках идут координаты (Xi, Yi) вершин многоугольника в порядке обхода по часовой стрелке. Xi и Yi - целые числа, по модулю не превосходящие 1000000.
Выведите одно число - искомое количество точек.
4 1 1 1 2 2 2 2 1
0
Первый учебный день шестиклассника Пети начался с урока географии. Учитель объяснял классу, что перед тем, как изучать просторы нашей Родины, нужно научиться пользоваться географическими картами. Было также упомянуто и о том, что такое масштаб карты. В качестве домашней работы Пете и его одноклассникам задали нарисовать план (карту) своей комнаты, соблюдая масштабирование. Петю очень заинтересовало задание учителя, и поэтому, как только он пришел из школы домой, он принялся рисовать план. Это занятие было очень увлекательным, но вскоре с работы пришла Петина мама, сказала, что здоровье превыше всего и позвала его обедать. Во время обеда она по пути на кухню зашла в Петину комнату и решила, что ее надо проветрить. Для этого она открыла окно, перед которым стоял Петин стол.
Насытив свой желудок, Петя вернулся в комнату и обнаружил, что его творение сдуло ветром на пол. Сначала он обеспокоился тем, в порядке ли рисунок, но удостоверившись, что все нормально, не стал спешить и поднимать план с пола. Он вспомнил слова учителя географии, который в конце урока поведал им некое нетривиальное утверждение и предложил любопытным проверить его на досуге.
Утверждение гласило: "если взять две карты одной и той же области, сделанные с разным масштабом, и расположить меньшую поверх большей так, что меньшая карта окажется строго внутри большей, то можно найти такую точку (она называется "неподвижная точка"), что то, что изображено в этой точке на обеих картах соответствует одной и той же точке местности". Петя заметил, что пол комнаты можно считать картой комнаты (масштаб 1:1). Он решил найти неподвижную точку для лежащего на полу нарисованного им плана и пола. Но Петя не сумел сделать это самостоятельно, поэтому он обратился к вам за помощью.
Комната Пети и ее план имеют форму прямоугольника. Первая строка входного файла содержит два вещественных числа: ширину X и длину Y комнаты Пети (1≤X≤1000, 1≤Y≤1000). Комната расположена в декартовой прямоугольной системе координат так, что углы комнаты расположены в точках с координатами (0,0), (X,0), (X,Y), (0,Y).
Вторая строка содержит восемь вещественных чисел, описывающих положение углов плана комнаты в той же самой системе координат. Сначала задаются координаты того угла плана, который соответствует углу комнаты с координатами (0,0), затем — (X,0), (X,Y), наконец, (0,Y). Гарантируется, что входные данные корректны, то есть план является прямоугольником, линейные размеры плана находятся в полном соответствии с линейными размерами комнаты, план не выходит за границы комнаты.
Все числа во входном файле вещественные, заданы с точностью 5 знаков после десятичной точки. План выполнен в масштабе не менее 0.0001 и не более 1. Масштаб не может быть равен 1. Карта расположена лицевой стороной вверх.
В первую строку выходного файла выведите 2 вещественных числа — координаты неподвижной точки плана и пола. Ответ нужно выдать с 3 знаками после десятичной точки.
10.00000 5.00000 3.00000 2.50000 1.00000 2.50000 1.00000 1.50000 3.00000 1.50000
2.500 2.083
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
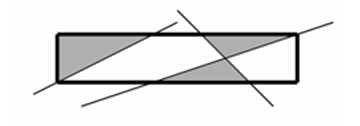
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала вводятся два положительных числа X, Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее записано целое число N - количество разрезов (1≤N≤200). Далее описываются сами разрезы. Все разрезы делались вдоль прямых. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все вводимые числа (кроме N) вещественные, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число - количество частей исходного прямоугольника, имеющих треугольную форму.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4