Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
Дано \(N\) точек на плоскости, их надо покрасить в черный и белый цвета.
При этом должны присутствовать точки обоих цветов и должна существовать прямая, по одну сторону от которой все точки черные, по другую белые.
Требуется посчитать количество раскрасок, удовлетворяющих этим условиям.
В первой строке задано число \(2 \leq N \leq 300\). В следующих \(N\) строках заданы координаты точек.
Выведите единственное число - количество различных раскрасок.
4 0 0 1 0 1 1 0 1
12
3 0 0 0 1 0 2
4
В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.
Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.
На вход сначала подается число n — количество ульев (\(1 \leq n \leq 200\)).
Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих \(n\) строках входных данных записаны координаты ульев в саду Бена. Они не превосходят \(10000\) по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от \(1\) до \(n\).
Следующие \(n\) строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.
Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.
3 1 0 1 1 0 1 0 2 1 2 1 3
0 3
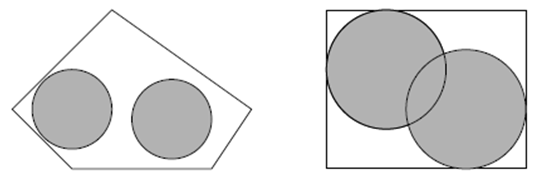
Фен шуй – это древняя китайская практика размещения предметов в пространстве для достижения гармонии. В ней говорится, что пол не должен быть пустым, поэтому Фил разместил на полу два одинаковых круглых ковра (по фен шуй надо избегать прямых линий и острых углов).
К сожалению, ими нельзя покрыть пол комнаты полностью, так как она имеет форму выпуклого многоугольника. Фил хочет минимизировать непокрытую часть пола, располагая ковры оптимальным образом.
Помогите ему расположить два ковра в комнате так, чтобы общая покрытая площадь была максимальна. Ковры можно накладывать друг на друга, но их нельзя загибать и резать.
Первая строка входных данных содержит два целых числа \(n\) и \(r\) — число углов в комнате \((3 \le n \le 100)\) и радиус ковров (\(1 \le r \le 1000\), оба ковра имею один и тот же радиус). Следующие n строк содержат по два числа \(x_i\) и \(y_i\) — координаты \(i\)-го угла \((–1000 \le x_i; y_i \le 1000). Углы описаны в порядке обхода комнаты по часовой стрелке. Координаты углов различны и соседние стены не коллинеарны.
Выведите \)x_1, y_1, x_2, y_2\(, где \)(x_1, y_1)\( и \)(x_2, y_2)$ обозначаю центры ковров. Координаты должны иметь точность не менее 4 цифр после точки. Выведите любое оптимальное расположение. Входные данные гарантируют, что решение существует (Фил не стал бы покупать ковер, который не помещается в комнату).
5 2 -2 0 -5 3 0 8 7 3 5 0
-2.1715728753 3.0000000000 4.2617090669 2.4981148759
4 3 0 0 0 8 10 8 10 0
3.0000000000 5.0000000000 7.0000000000 3.0000000000
На плоскости задано N векторов. Есть 3 правила:
1) вектора на непересекающихся прямых можно сложить
2) вектора на одной прямой можно сложить (результат исходит из начала одного из векторов)
3) в любой точке можно породить два одинаковых по длине, но разнонаправленных вектора
Требуется найти эквивалентную данной систему, содержащую минимальное количество векторов.
На плоскости задано N векторов – направленных отрезков, для каждого из которых известны координаты начала и конца (вектор, у которого начало и конец совпадают, называется нуль-вектором, можно считать, что нуль-вектор лежит на любой прямой, которая через него проходит). Введем следующие три операции над направленными отрезками на плоскости:
1) Направленные отрезки ненулевой длины, лежащие на пересекающихся прямых, можно заменить на их сумму, причем единственным образом. В этом случае отрезки переносятся вдоль своих прямых так, чтобы их начала совпадали с точкой пересечения прямых, и складываются по правилу сложения векторов (правилу параллелограмма, при этом началом результирующего вектора является точка пересечения прямых).
2) Направленные отрезки, лежащие на одной прямой, также можно заменить на их сумму. Для этого один из отрезков (любой) нужно перенести в начало второго из них и сложить по правилу сложения векторов на прямой:
Это правило применимо и в случае, когда один из векторов, или даже оба, являются нуль-векторами.
Заметим, что если складываемые векторы противоположно направлены и имеют одну и ту же длину, то результатом их сложения является нуль вектор.
3) В любой точке плоскости можно породить два противоположно направленных отрезка равной (в том числе и нулевой) длины:
Будем говорить, что две системы векторов эквивалентны, если от одной системы можно перейти к другой с помощью конечной последовательности перечисленных выше операций.
Требуется получить любую систему векторов, эквивалентную заданной, состоящую из как можно меньшего числа векторов.
В первой строке входного файла записано число N – количество заданных векторов (1 < N ≤ 1000). В каждой из следующих N строк через пробел записаны четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – целые числа, по модулю не превосходящие 1000.
В первой строке входного файла следует записать число M – количество векторов в полученной системе (1 ≤ M ≤ N). В каждой из следующих M строк через пробел должны находиться четыре числа, обозначающие координаты начала и конца каждого из векторов соответственно. Все координаты – вещественные числа, записанные с 6 цифрами после точки.
3 1 1 1 3 3 3 3 1 5 1 7 1
1 3.000000 3.000000 5.000000 3.000000
2 2 4 5 10 -2 -4 -5 -10
1 2.000000 4.000000 2.000000 4.000000
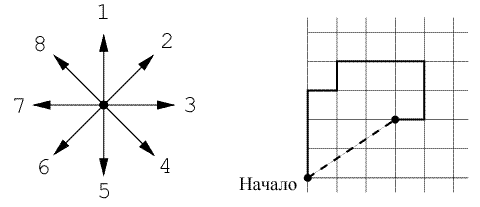
Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм нахождения клада так: «Встаньте около одинокой пальмы. Пройдите тридцать шагов в сторону леса, потом семнадцать шагов в сторону озера, …, наконец десять шагов в сторону большого булыжника. Клад находится под ним». Большая часть таких указаний просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.
Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рис).
Вам необходимо написать программу, которая по указаниям пиратов определяет точку, где зарыт клад.
Первая строка входного файла содержит число N – число указаний (1≤N≤40). Последующие N строк содержат сами указания – номер направления (целое число от 1 до 8) и количество шагов (целое число от 1 до 1000). Числа разделены пробелами.
В выходной файл выведите координаты X и Y точки (два вещественных числа, разделённые пробелом), где зарыт клад, считая, что ось Ox направлена на восток, а ось Oy – на север. В начале кладоискатель должен стоять в начале координат. Координаты необходимо вывести с погрешностью не более 10-3.
6 1 3 3 1 1 1 3 3 5 2 7 1
3.000 2.000
1 8 10
-7.071 7.071