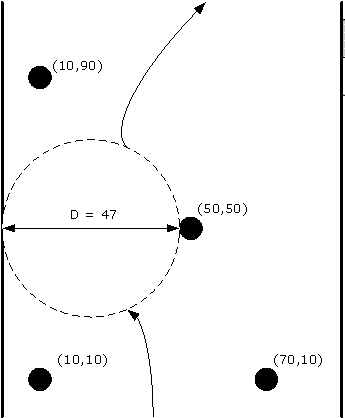Единственный способ попасть в Зал Круглых Столов – пройти через Колонный Коридор. Стены Коридора изображаются на карте прямыми линиями, которые параллельны оси OY системы координат. Вход в Коридор находится снизу, а выход из Коридора в Зал – сверху. В Коридоре есть цилиндрические (на карте круглые) Колонны одинакового радиуса R.
Напишите программу, которая по информации о размерах Коридора, и размещения Колонн определяет диаметр наибольшего из Круглых Столов, который можно пронести через такой Коридор, сохраняя поверхность Стола горизонтальной.
В первой строке входного файла заданы два числа XL и XR – x-координаты левой и правой стен Коридора. Во второй строке находится целое число R (1≤R≤1 000 000) – радиус всех Колонн. В третей – целое число N (1≤N≤200), которое задает количество Колонн. Далее следуют N строк, в каждой из которых по два числа – x- и y-координаты центра соответствующей Колонны.
Все входные координаты – целые числа, которые по модулю не превосходят 1 000 000.
Единственная строка выходного файла должна содержать одно число – искомый диаметр наибольшего Стола. Диаметр следует выводить с точностью 3 знака после десятичной точки (даже в случае, когда он окажется целым). Если нельзя пронести ни одного Стола, то ответ должен быть: 0.000
Точность 3 знака после точки, по обычным правилам округления, обозначает, что ответ, который выдается в выходной файл, должен отличаться от точного не более чем на 510-4 (т.е. на 0.0005). Например, если точный ответ 1.234567, то в файле должно находится число 1.235. Если точный ответ 5.0005, то необходимо округлять в большую сторону, т.е. в файл следует выдать 5.001
0 90 3 4 10 10 70 10 50 50 10 90
47.000
С незапамятных времен граница страны Флатландия имеет форму N-угольника без самопересечений и самокасаний (необязательно выпуклого). В каждой из вершин этого многоугольника король построил по башне.
В целях увеличения обороноспособности государства на его территории король задумал построить Великий Флатландский Забор. По причине многолетней войны ресурсов хватает на строительство ровно K стен (неважно, какой длины). Каждая стена должна соединять ровно две башни по прямой и не должна даже частично выходить за пределы Флатландии. К тому же, Забор должен представлять собой не более чем K-угольник также без самопересечений и самокасаний (углов может оказаться и меньше, чем K, так как некоторые соседние стены могут лежать на одной прямой). Военный советник настаивает на том, что площадь защищенной области должна быть как можно больше.
Ваша задача — помочь спроектировать такой Забор.
В первой строке записаны два целых числа N и K (3 ≤ K ≤ N ≤ 230). В следующих N строках содержатся пары целых чисел — координаты башен в порядке обхода границы против часовой стрелки. Гарантируется, что никакие три последовательные башни не лежат на одной прямой. Все координаты не превосходят 1000 по абсолютной величине.
В первую строку запишите максимальную площадь, которую можно защитить Забором, с точностью до пяти знаков после десятичной точки. Во второй строке должно быть Q — количество выбранных башен.
Будем считать, что башни занумерованы числами от 1 до N в порядке перечисления их во входном файле. Во третью строку через пробел выведите номера Q башен, которые будут вершинами Забора, в порядке его обхода против часовой стрелки.
Частичные ограничения
Первая группа состоит из тестов, в которых N ≤ 20 и граница Флатландии представляет собой выпуклый многоугольник.
Вторая группа состоит из тестов, в которых N ≤ 20, но граница может быть уже любой.
3 3 0 0 1 0 0 1
0.50000 3 1 2 3
6 5 0 0 7 0 4 3 4 4 3 4 0 7
24.50000 5 1 2 3 5 6
4 3 0 0 1 3 0 2 -2 -2
2.00000 3 1 3 4
На плоскости заданы N разных окружностей. Две окружности пересекаются, если они имеют хотя бы одну общую точку.
Напишите программу, которая по координатам центров окружностей и их радиусам найдет пару пересекающихся окружностей.
В первой строке входного файла содержится целое числоN (1≤N≤10 000) . В каждой из последующих N строк содержатся три натуральных числа X, Y, R меньших 10 000, которые задают координаты центра окружности (X, Y) и его радиус R.
Единственная строка выходного файла должна содержать пару номеров пересекающихся окружностей, либо единственное число 0, если никакие две окружности не пересекаются. Окружности нумеруются соответственно порядку во входном файле, начиная с 1 до N. Если существует несколько пар пересекающиеся окружностей, выведите любую из них. Элементы пары могут быть выведены в произвольном порядке.
5 5 10 4 6 20 3 10 15 3 12 8 2 13 13 1
5 3
В руки одного искателя приключений попал старинный пиратский манускрипт. В рукописи сказано: "Придя на восходе солнца в точку \(A\), я начал свой путь по острову в поисках надежного места, чтобы спрятать сокровища. Я шел не спеша, все время с одинаковой скоростью в том направлении, куда показывала моя тень. Двигаясь таким образом, через \(N\) часов я вышел к руинам какого-то древнего храма, у северо-западного угла которых я и закопал свои сокровища. Вернувшись на корабль к заходу Солнца я с удивлением обнаружил, что в этот день от восхода Солнца до его захода прошло ровно 12 часов, причем Солнце взошло точно на востоке, а село точно на западе."
Искатель приключений, конечно же пожелал найти сокровища. Тем более, что число N ему было известно, а изображение точки A на карте прекрасно сохранилось. Единственная проблема – на острове оказалось слишком много разных руин, и исследовать их все займет очень много времени.
Напишите программу, которая по описанию острова определит список руин, наличие клада у которых наиболее вероятно. При решении задачи будем считать что угловая скорость Солнца над горизонтом постоянна (то есть за одно и то же время Солнце проходит один и тот же угол).
сначала вводится число \(N\) (натуральное, не превышает 11), затеем число \(k\) (натуральное, не превышает 100). Далее следует k строк по 3 числа в каждой – координаты и радиус соответствующих руин (целые, по модулю не превышают 1000). Гарантируется что никакие руины не перекрываются. Координатная плоскость организована таким образом: за начало координат принята точка \(A\), ось \(O_Y\) направлена с юга на север, ось \(O_X\) направлена с запада на восток.
выведите список руин, в которых следует искать клад, упорядоченный по удаленности от точки \(A\). В списке следует выводить только координаты руин, по одному объекту в строке. Гарантируется, что на острове существуют хотя бы одни искомые руины.
6 3 -100 0 10 0 100 10 -50 50 20
-50 50
Дан выпуклый четырехугольник ABCD с ненулевой площадью. Найти точку O, принадлежащую какой-либо стороне четырехугольника, что площади фигур, полученных в результате разреза исходного четырехугольника по линии AO, были бы равны.
вводятся координаты 4 точек (целые, по модулю не превышают 100). Гарантируется, что никакие три точки не лежат на одной прямой.
вывести координаты точки O с точностью до 4 знака после запятой.
0 0 1 1 0 2 -1 1
0 2