Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
На территории будущей стройки растут три дерева. Фирма получила разрешение на строительные работы с условием, что два (любых) дерева будут сохранены. Прораб хочет построить забор треугольной формы так, чтобы внутри него оказалось ровно два дерева.
Деревья на плане изображаются кругами, которые попарно не вложены друг в друга и не пересекаются (но могут касаться).
Напишите программу, которая по введенной информации о деревьях определит, возможно ли построить такой забор, и, если да, то какое дерево окажется не огорожено.
Вводится информация о трех деревьях: для каждого дерева координаты центра и радиус круга, изображающего это дерево на плане. Все числа целые, не превосходящие по модулю 3000. Радиус – натуральное число.
Выведите одно число – номер дерева (деревья нумеруются начиная с 1 в порядке задания их во входных данных), которое окажется не огорожено. Если забор треугольной формы, огораживающий ровно два дерева, построить невозможно, выведите число 0. Если существует несколько решений, выведите любое.
Как известно, к северу от Москвы находится много горнолыжных трасс, расположенных на холмах Клинско-Дмитровской гряды. Один из курортов в связи с финансовым кризисом решил расширить спектр услуг, предлагая трассы для катания не только на лыжах и сноубордах, но и санные трассы.
У хозяев курорта имеется топографическая карта территории, высоты на которой отображены с помощью контуров, каждый из которых представляет собой окружность. У каждой окружности указана высота поверхности, прилегающей к внутреннему контуру этой окружности. Вся территория, которая не находится внутри какой-либо окружности, имеет высоту 0. Поскольку это единственная информация о местности, то можно условно считать, что участки между окружностями плоские. Никакие две окружности не пересекаются и не касаются.
Используя эту карту, необходимо проложить санную трассу, которая будет удовлетворять двум условиям: разница высот между начальной и конечной точками должна быть максимальна, и количество пересекаемых контуров не должно превышать некоторого заданного значения \(K\) (это связано с тем, что то место, которым сидят на санках, имеет ограниченную прочность). При этом трасса может иметь участки подъема, но не должна включать в себя ни одной точки, которая была бы выше начальной (туда санки просто не заедут).
На приведенном рисунке пунктирной линией показана наилучшая трасса для \(K\) = 4. Разница высот в ней составляет 68.
Сначала вводятся два натуральных числа \(C\) (1 ≤ \(C\) ≤ 2 000) — количество окружностей и \(K\) (1 ≤ \(K\) ≤ 2 000) – максимальное количество окружностей, которое может пересечь трасса.
Далее идут описания окружностей, каждое из которых состоит из четырех целых чисел: \(X\), \(Y\) (–2000 ≤ \(X\) ≤ 2000, –2000 ≤ \(Y\) ≤ 2000) – координаты центра окружности, \(R\) (1 ≤ \(R\) ≤ 2000) — радиус окружности и \(A\) (–1000 ≤ \(A\) ≤ 1000) — высота местности, касающейся внутреннего края окружности.
Выведите одно число — максимальный перепад высот на трассе.
Пример
| Входные данные | Выходные данные |
| 10 4 38 61 2 73 69 34 3 15 61 59 4 30 40 60 5 66 58 44 6 30 71 34 6 -2 47 21 6 45 41 58 8 52 41 57 11 37 48 40 33 10 | 68 |
На плоскости задано N (1 ≤ N ≤ 30) супермногоугольников (без пересечений и самопересечений). Каждый супермногоугольник задаётся координатами своих Ki (3 ≤ Ki ≤ 30, 1 ≤ i ≤ N) вершин в порядке обхода против часовой стрелки. Все координаты — целые числа из диапазона -32000..32000. Требуется соединить супермногоугольники М отрезками так, чтобы:
Oтрезок соединяет только пару супермногоугольников.
Суммарная длина отрезков была минимальна.
Между любыми двумя супермногоугольниками должен существовать путь (последовательность некоторых отрезков и частей границ супермногоугольников).
Формат входных данных
В первой строке число N. В следующих N строках. Число Ki и Ki пар чисел – координаты вершин.
Формат выходных данных
В первой строке число М и сумма длин найденных отрезков с точностью 10-3. В следующих М строках числа L1 X1 Y1 L2 X2 Y2 – номера супермногоугольников и координаты концов отрезков с точностью 10-3.
Примеры
| Входные данные | Выходные данные |
| 2 3 1 0 2 0 1 1 4 6 5 7 5 7 6 6 6 | 1 6.364 1 1.500 0.500 2 6.000 5.000 |
| 3 3 0 0 1 0 0 1 4 5 5 6 5 6 6 5 6 3 0 5 1 6 0 6 | 2 8.000 3 1.000 6.000 2 5.000 6.000 1 0.000 1.000 3 0.000 5.000 |
Вводится новый авиарейс между городами \(A\) и \(B\). Самолет будет лететь строго по прямой, соединяющей эти города. На протяжении всего пути необходимо, чтобы за самолетом могли наблюдать с земли при помощи радаров. Однако, радиус действия радаров ограничен, и равен \(R\). Хуже того, радарные станции имеются только в определенных точках (например, других населенных пунктах). Руководство авиакомпании желает выяснить: можно ли следить за самолетом на протяжении всего пути из \(A\) в \(B\). Если это возможно, то каким минимальным количеством уже имеющихся радаров можно для этого обойтись. Самолет, находящийся на границе действия радара является видимым, то есть если расстояние от радара до самолета точно равно \(R\), то считается что радар еще действует.
сначала вводятся координаты точек \(A\) и \(B\) (целые числа, по модулю не превышают 1000), затем вводится число \(N\) (натуральное, не превышает 20) – количество уже построенных радаров, затем следует число \(R\) – радиус действия радара (натуральное, не превышает 1000). Затем вводится \(N\) пар чисел – координаты уже построенных радаров (целые, по модулю не превышают 1000). Наличие радаров в городах \(A\) и \(B\) возможно, но необязательно.
выведите минимальное количество радаров, которое надо задействовать для сопровождения самолета на всем пути. Если сопровождение имеющимися средствами невозможно – выведите число -1.
0 0 1 1 1 1 5 5
-1
0 0 10 0 3 5 0 0 5 0 10 0
1
Михаил — маг 80-го уровня. Одно из его изобретений — лабиринт, который дает сверхспособности каждому, кто проходит через него. Лабиринт имеет очень сложную магическую структуру, но внешне выглядит как квадрат, нарисованный на земле.
Михаил нашел подходящее место для лабиринта на берегу Клязьмы. Он нарисовал границу лабиринта палочкой на песке и отметил 4 точки на границах лабиринта так, что на каждой из сторон лабиринта лежал камень и ни один камень не лежал в углу.
В нашем мире все течет и меняется: река Клязьма по весне разлила свои воды, затопив пляж. Изображение на песке стерлось, остались только лежащие камни. Теперь Михаил не может восстановить свой лабиринт.
За помощь в восстановлении лабиринта Михаил обещал научить вас вставлять палочку в одно ухо и вынимать из другого.
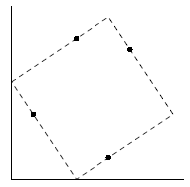
В четырех строках входного файла содержатся координаты камней \(x_i\) и \(y_i\) (-1000 ≤ \(x_i\), \(y_i\) ≤ 1000). Точки не совпадают и никакие три точки не лежат на одной прямой.
Выведите четыре строки, каждая из которых содержит два вещественных числа — координаты вершин квадрата. Вершины должны быть перечислены в порядке обхода по или против часовой стрелки. Числа необходимо выводить с точностью 6 знаков после точки. Если решений несколько — выведите любое из них. Если решений нет — выведите 4 пары нулей
6 13 11 12 9 2 2 6
9.0 15.0 15.0 6.0 6.0 0.0 0.0 9.0
0 0 5 5 5 0 3 2
0 0 0 0 0 0 0 0