Движением плоскости называют такое преобразование плоскости, которое сохраняет попарные расстояния между точками, то есть если \(A_1\) и \(B_1\) – образы некоторых точек \(A\) и \(B\) при движении, то \(|A_1 B_1| = |AB|\).
Одной из разновидностей движения плоскости является скользящая симметрия. Скользящей симметрией называют композицию симметрии относительно некоторой прямой \(l\) и переноса на вектор, параллельный \(l\) (этот вектор может быть нулевым). На рисунке показан пример применения скользящей симметрии к отрезку.
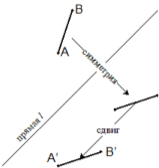
Известно, что любой отрезок можно перевести в любой другой отрезок такой же длины с помощью скользящей симметрии. Требуется по координатам двух различных точек \(A\) и \(B\) и двух точек \(A_1\) и \(B_1\), находящихся на таком же расстоянии друг от друга, как и точки \(A\) и \(B\), найти скользящую симметрию, переводящую точку \(A\) в точку \(A_1\), а точку \(B\) в точку \(B_1\).
В первой строке входного файла находятся четыре целых числа – координаты двух различных точек \(A\) и \(В\). Во второй строке также находятся четыре целых числа – координаты двух различных точек \(A_1\) и \(В_1\). Гарантируется, что \(|A_1B_1| = |AB|\). Все числа во входном файле по модулю не превышают \(1000\). Числа в строках разделены пробелом.
Выведите в выходной файл описание искомой скользящей симметрии, которое представляется в следующем виде.
В первой строке должны выводиться координаты двух различных точек, лежащих на прямой \(l\), относительно которой выполняется симметрия, а во второй – координаты вектора, параллельного этой прямой, на который осуществляется перенос. Вещественные числа должны быть представлены не менее чем с 6 знаками после десятичной точки.
Вася с Петей играют в интересную игру. Правила ее очень простые: есть две рамки и участники должны передвинуть вторую рамку так, что площадь пересечения рамок была бы как можно большой. Оба игрока думают в течение минуты и записывают вектор переноса второй рамки. Побеждает тот игрок, чей вектор переноса дал большую площадь пересечения.
Игра имеет много частных случаев, так что Вася решил сжульничать и написать программу, находящую лучший вектор переноса.
В этой игре рамкой называется фигура, состоящая из двух прямоугольников: внешнего и внутреннего. Внутренний прямоугольник лежит строго внутри внешнего. Стороны обоих прямоугольников параллельны координатным осям.
На первом рисунке указаны (1) неправильные рамки, (2) правильные рамки, (3) пересечение рамок.
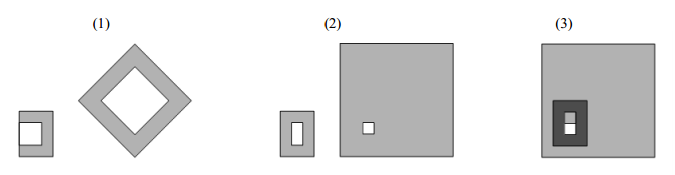
Площадь рамки вычисляется как W∙H – w∙h, где W, H – размеры внешнего прямоугольника, а w, h - размеры внутреннего (0 < w < W; 0 < h < H).
Напишите программу, которая находит перенос одной рамки относительно другой, которая даст максимальную площадь пересечения.
Каждая рамка описывается с помощью четырех точек — двух противоположных углов внешнего прямоугольника и двух противоположных углов внутреннего прямоугольника. Точки описываются своими координатами x и y, которые являются целыми числами и не превосходят 108 по модулю.
В первой строке содержится описание первой рамки, во второй — второй.
Первая строка выходного файла должна содержать целое число A – максимальная площадь области пересечения данных рамок достижимая с помощью переноса.
Вторая строка должна содержать пару целых чисел x и y – координаты вектора переноса второй рамки который даст область пересечения A. Координаты не должны превосходить 1018 по абсолютному значению.
2 2 5 6 3 3 4 5 0 0 10 10 2 2 3 3
10 0 -4
Роботы начинают все чаще использоваться в домашнем хозяйстве. Один программист решил сделать робота для своих хозяйственных нужд. Как известно, многие программисты потребляют напиток "Живчик", от которого на столе остаются разбросанные пустые бутылки. Поэтому он решил запрограммировать робота собирать пустые бутылки со стола.
Стол имеет форму прямоугольника длиной l и шириной w. Робот стартует в точке xr, yr, а N бутылок расположены в точках xi, yi (для i от 1 до N).
Чтобы убрать бутылку робот должен дойти до нее, взять ее, донести до любого края стола и сбросить. Робот может держать только одну бутылку, поэтому убирает он их по очереди.
Размером робота и бутылок можно пренебречь, в том числе можно считать что робот свободно может пройти мимо любой бутылки. Напишите программу, которая определяет минимальную длину пути робота, который ему необходимо пройти, чтобы убрать все бутылки со стола.
Первая строка входного файла содержит два целых числа w и l. (2 ≤ w, l ≤ 1000). Вторая строка входных данных содержит N – число бутылок на столе (1 ≤ N ≤ 18). Каждая из следующих N строк содержит два целых числа xi, yi – координаты i-й бутылки на столе (0<xi<w; 0<yi<l). Никакие две бутылки не находятся в одной точке.
Последняя строка входного файла содержит 2 целых числа xr, yr – координаты начальной позиции робота (опять же не у края стола и не в точке с бутылкой).
Выведите длину кратчайшего пути робота с точностью не менее 6 значащих цифр после точки.
3 4 2 1 1 2 3 2 1
5.60555127546399