Элементарная геометрия(144 задач)
Многоугольники. Выпуклые оболочки(38 задач)
Клеточная геометрия(8 задач)
Квадродерево(3 задач)
В плоской стране все было как в настоящей, только плоское, и люди и горы и все, все, все. Жили в этой стране люди хорошие, но иногда попадались преступники и тогда их отвозили на плоский остров и там оставляли поразмыслить о жизни. А чтобы они не сбежали с острова, было решено построить наблюдательную вышку, с которой можно было бы следить за преступниками. Но, так как жители страны были плоскими, то и мозги у них были тоже плоскими и никак они не могли определить, в каком месте построить вышку и какой высоты. Помогите им. Вам предлагается найти самую низкую точку — координаты верхней точки вышки (плоские люди были экономными), из которой видно крайние точки острова, и найти высоту вышки. Как выяснили плоские ученые, профиль острова позволял построить вышку высотой не более 20000 метров. Профиль острова — это ломаная, имеющая примерно такой же вид как на рисунке. На острове нет лагун и с каждой вершины видны оба склона этой вершины. Точки С и Д — это крайние точки острова. 
Файл входных данных в первой строке содержит одно натуральное число N — количество вершин ломаной, не считая концов A и B. (1 ≤ N ≤ 1000) Во второй строке четыре целых числа x1, y1, x2, y2 — координаты точек A и B. ( - 1000 ≤ xi, yi ≤ 1000) В последующих N строках по два целых числа — координаты вершин xi, yi ломаной, данных в порядке обхода от А к В.( - 1000 ≤ xi, yi ≤ 1000)
Выходной файл должен содержать в первой строке два вещественных числа — координаты вершины вышки, во второй строке одно вещественное число — высоту вышки. Все числа с тремя знаками после десятичной точки. Если ответов несколько, то выведите самый левый из них.
3 0 0 100 0 20 20 40 20 70 30
50.000 50.000 26.667
Мэр одного большого города решил ввести плату за проезд по шоссе, проходящим в районе города, чтобы снизить объем транзитного транспорта. В районе города проходит n шоссе.
Но руководство области, в которой расположен город, воспротивилось планам мэра. Действительно – дальнобойщики представляют собой неплохой источник доходов для большого количества кафе и гостиниц в небольших городках.
В результате решили, что плата будет введена только на шоссе, которые проходят через город.
В городе используется развитая система метрополитена, всего в городе есть m станций метро. Решено было, что шоссе проходит через город, если либо одна из станций метро расположена непосредственно на шоссе, либо есть хотя бы одна станция с каждой стороны от шоссе.
Помогите теперь мэру определить, какие шоссе проходят через город.
Первая строка входного файла содержит два целых числа: n и m – количество шоссе и количество станций метро, соответственно (1 ≤ n, m ≤ 100 000).
Следующие n строк описывают шоссе. Каждое шоссе описывается тремя целыми числами a, b и c и представляет собой прямую на плоскости, задаваемую уравнением a×x+b×y+c = 0 (|a|, |b|, |c| ≤ 106). Следующие m строк входного файла описывают станции метро. Каждая станция описывается двумя целыми числами x и y и представляет собой точку на плоскости с координатами (x, y) (|x|, |y| ≤ 106).
Первая строка выходного файла должна содержать одно целое число – количество шоссе, которые проходят через город. Вторая строка должна содержать номера этих шоссе в возрастающем порядке. Шоссе нумеруются от 1 до n в порядке, в котором они описаны во входном файле.
Система тестов состоит из двух групп:
В тестах первой группы выполняется ограничение \(n \le 10^4\). За прохождение этой группы ставится 50 баллов.
В тестах второй группы дополнительных ограничений нет. За прохождение этой группы ставится также 50 баллов.
4 2 0 1 0 1 0 1 1 1 0 1 1 -1 0 0 2 0
3 1 3 4
Лена играет в машинки. Для этого она вырезала из бумаги машинку (являющуюся многоугольником без самопересечений и самокасаний) и стала возить её по столу. К сожалению, во время игры она разлила чай и на столе образовалась река. Для того, чтобы продолжить игру, Лене нужно провезти машинку через реку. Для этого она решила построить мост — длинную ленту, по которой и поедет машинка. На столе машинку можно поворачивать на любой угол, но для того, чтобы проехать через реку, её границы не должны выходить за границы моста. Ниже расположена фотография игрового поля и предполагаемое решение проблемы. Лене стало интересно — какой минимальной ширины может быть мост, чтобы машинка смогла проехать через реку?
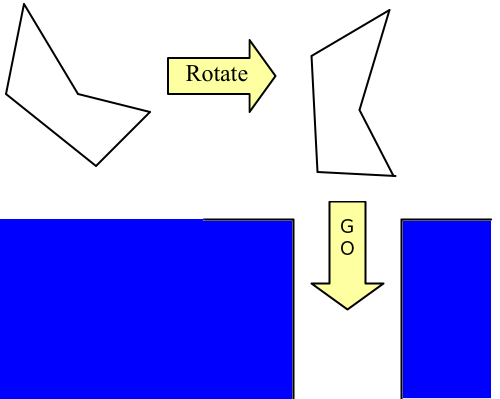
Внезапно Лена задумалась — ведь эта игра может стать прекрасной задачей по информатике, достойной финала международной студенческой олимпиады! Её Вам и предстоит решить.
Первая строка входного файла содержит T (Первая группа тестов: 0 < T < 11, вторая группа тестов: T = 1) -- количество тестов во входном файле. Далее следуют T тестов. Первая строка теста содержит число N (Первая группа тестов: 3 <= N <= 100. Вторая группа: 3 <= N <= 2 * 105) — количество вершин многоугольника.
Следующие N строк содержат по два числа — xi и yi (Первая группа тестов: 0 <= xi, yi <= 1000. Вторая группа: -105 <= xi, yi <= 105), задающие координаты многоугольника в порядке обхода. Гарантируется, что он не имеет самокасаний и самопересечений.
Для каждого теста на новой строке выведите одно число c точностью до двух знаков округляя в большую сторону — минимально требуемую ширину моста, при которой машинка сможет проехать через реку.
2 3 0 0 3 0 0 4 4 0 10 10 0 20 10 10 20
2.4000 14.1422
«И молвил тогда Король: Ты храбро сражался, Рыцарь, и твой подвиг не будет забыт в веках. За доблесть твою я дарую тебе сей замок и земли вокруг него. Однако нарушен был тобой строжайший из запретов все войны видели, как ты сражался без Шляпы на голове подобно дикарям, и их злые духи могли вселиться в тебя. Ты знаешь, что закон предков велит отправлять на небеса души подобных тебе, пока зло, которое могло укорениться в них, не вырвалось наружу. Но в моей воле пощадить тебя, ибо я вижу, что ты достаточно силен чтобы не позволить этому злу проникнуть в мысли и душу твои. Ты должен дать обет три месяца и три дня не покидать своей земли и каждый день три часа после захода солнца молить добрых духов о защите. Дела торопят меня, и не могу я препроводить тебя до замка. Поэтому я дарую тебе и дорогу от этого места до замка. А сейчас иди, и возвращайся по истечении срока.»— так записано в Зеленой Книге Лет.
Помимо этого из Зеленой Книги Лет известно, что земли, вместе с которыми был дарован замок, имели форму круга. Король был очень мудр и, во избежание лишних разбирательств относительно права на землю всегда даровал только области земли, на карте имеющие выпуклую форму. Недавно в распоряжении историков оказалась информация о том, где располагался замок и где происходил этот исторический разговор. Их интересует, участок земли какой площади получил Рыцарь в предположении, что дорога до замка была идеально прямой.

Первая входного файла содержит два вещественных числа xk и yk координаты места, в котором происходил диалог. Во второй строке записаны три вещественных числа xc , yc и rc координаты замка и радиус окружности, ограничивающей дарованную вместе с ним землю. Все числа во входном файле по модулю не превосходят 10000.
В выходной файл выведите одно вещественное число — площадь земельного участка, полученного Рыцарем, с точностью не менее трех знаков после десятичной точки.
1440.82150 -499.96180 975.76735 -128.57330 297.57553
338836.3611315
Недавно админ Вася настраивал компьютеры, в отделе Инопланетных объектов, увидел на столе спутниковый снимок с одной из недавно разведанных планет. На снимке было изображено необычное поле, разбитое на правильные шестиугольники, причем кто-то из ученых уже занумеровал все шестиугольники определенным образом.

На некоторых позициях, находились странные сооружения - шестиугольные башни, испускающие лучи в направлениях 6 соседних клеток. В этот момент, к столу подошел один из работников отдела. Очевидно, заметив любопытство Васи, он решил рассказать ему о находке. Оказывается, что эти самые лучи при пересечении излучают энергию, и чем больше лучей пересекается в одной точке, тем больше энергии излучается. При этом лучи идут по прямой очень далеко(возможно даже уходят в бесконечность), но не могут проходить через препятствия, например другие сооружения.
Теперь ученые пытаются на основе этого открытия построить новый источник дешевой энергии, но для этого им нужно уметь находить для интересующей их точки, сколько лучей через нее проходят, и какие эмиттеры (странные шестиугольные сооружения) их излучают.
В первой строке указаны 3 числа n , r , c (1 ≤ n ≤ 10 5 , 0 ≤ r , c ≤ 10 9 ) - количество эмиттеров, и координаты интересующей ученых позиции. В следующих n строках указано по паре чисел r i , c i (0 ≤ r i , c i ≤ 10 9 ) , координаты i-ого эмиттера. Гарантируется, что никакие два эмиттера не находятся в одной точке, и никакой эмиттер не находится в интересующей ученых точке.
В первой строчке выходного файла выведите единственное число k — количество лучей проходящих через интересную точку.
В следующей строчке выведите k чисел, номера эмиттеров, излучающих эти лучи, в произвольном порядке(все эмиттеры занумерованы с 1)
4 2 2 0 0 0 3 2 1 3 3
2 3 2