Магическим квадратом называют таблицу, в которой записаны числа \(1, 2, 3, …\) по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной \((3\times 3, 5\times 5, …)\).

Поставим число \(1\) в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа \(2, 3, 4, …\). Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.

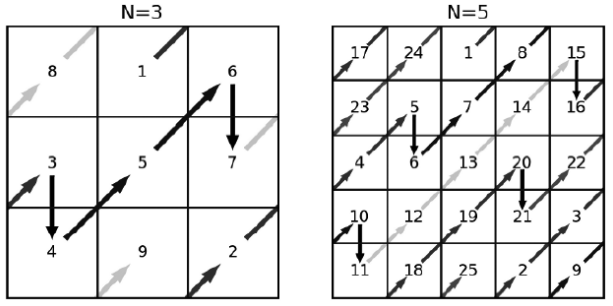
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов \(3\times 3\) и \(5\times 5\) показаны на рисунках.

По введенным значениям n, m (1 <= n <= 20, 1 <= m <= 20) заполните массив размерностью n x m числами от 1 до mn, расположив их по столбцам так, как показано в примере. Числа разделяйте одним пробелом.

Проводя генеральную уборку на дачном чердаке, Саша нашел в комоде кучу доминошек из разных наборов. Каждая доминошка представляет собой прямоугольник, разделенный на две половинки. На каждой из половинок нарисовано от 0 до 6 точек. Ориентации доминошки не имеют — их можно как угодно поворачивать.

В совсем раннем детстве Саша видел, как играют в домино: суть игры заключается в том, что надо брать доминошку и как можно громче колотить ею об стол, крича при этом «рыба!». Услышав доносящийся с чердака грохот, наверх поднялся Сашин дедушка. Он смог объяснить Саше настоящие правила игры в домино: игроки составляют длинную цепочку, в которой соседние доминошки касаются половинками с одинаковым числом точек.

Саше решил называть «дружными доминошками» пару доминошек, которые можно поставить в игре рядом (т.е. доминошки в паре соприкасаются половинками с равными числами) в том или ином порядке. Играть в домино ему не с кем, поэтому Саша развлекается тем, что всевозможными способами составляет пары и считает количество «дружных доминошек».

По заданному набору доминошек определите, сколько пар «дружных доминошек» можно составить из него. Пары, отличающиеся хотя бы одной доминошкой, считаются различными. По-разному составленная пара из одних и тех же доминошек считается один раз.