--->
118 задач
<---
Источники
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Поле Чудес представляет из себя прямоугольную грядку размером n × m лунок, в каждую из которых можно закопать одну монету. Буратино зарыл на Поле Чудес все имевшиеся у него монеты, благоразумно составив карту посадок – звездочками он отмечал лунки, в которых лежат монеты, а точками — лунки без монет.
Теперь его интересует вопрос: а каких лунок больше – с монетами или без? Сколько было у него монет, он, к сожалению, не помнит.
Помогите Буратино справиться с этой задачей.
Входные данные
В первой строке даны два целых числа n и m – размеры грядки ( 1 ≤ n , m ≤ 20 ). В следующих n строках по m символов перечисляется содержимое грядки (точками отмечена пустая лунка, звездочкой – с монетой).
Выходные данные
Выведите число 1, если лунок с монетами больше, чем пустых, число 2, если пустых лунок больше, чем полных и число 0, если их количества равны.
Примеры
Входные данные
3 3 **. .** *.*
Выходные данные
1
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Крокодил Гена с Чебурашкой играли в какую-то игру, выписывая числа в клетки квадратной таблицы n × n . Однако, когда таблица была заполнена целиком, выяснилось, что правила игры они забыли. Тогда Чебурашка предложил подсчитать числа на главной диагонали квадрата и на побочной диагонали, и если на главной диагонали сумма чисел больше, чем на побочной, то выигрывает Гена, если меньше, то Чебурашка, а если суммы равны, то объявляется ничья.
Таблица была большая и Чебурашка с Геной боятся ошибиться при подсчете. Помогите им определить, чем закончилась игра.
Входные данные
В первой строке дано одно целое число n – размер таблицы ( 1 ≤ n ≤ 20 ). Дальше идут n строк по n неотрицательных чисел в каждой – заполненная после окончания игры таблица. Все числа не превышают 100 .
Выходные данные
Выведите 1, если выиграл Крокодил Гена, 2, если выиграл Чебурашка, и 0, если была ничья
Примеры
Входные данные
3 1 2 3 4 5 6 7 8 0
Выходные данные
2
#112033
Темы:
[Двумерные массивы]
[Формула]
Источники:
[
Личные олимпиады,
Открытая олимпиада школьников,
2012-2013,
Заключительный этап - второй тур,
Задача B
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
Скоро в Берляндии пройдет очередная Олимпиада. В рамках подготовки к этому важному мероприятию Берляндолимпстрой уже возвел N объектов и теперь хочет разобраться с тем, во сколько Берляндии это обошлось.
Стройка длилась \(K + 1\) день со дня номер \(0\) по день номер \(K\), причем стоимость j-го объекта в нулевой день была равна \(a_j\) бурлям. Однако каждый следующий день стоимость каждого объекта увеличивалась согласно следующему правилу: стоимость j-го объекта в i-й день становилась равна сумме стоимостей всех объектов с номерами, меньшими или равными j, в предыдущий день. Иначе говоря, \(S_{i,j}\) = \(\sum_{m=1}^{j} S_{i-1,m}\), где \(S_{i,j}\) — стоимость j-го объекта в i-й день. В итоге на j-й объект было потрачено \(S_{K,j}\) , то есть его стоимость в последний \(K\)-й день. \t{Назовем эту величину итоговой стоимостью j-го объекта.}
Такие увеличения стоимостей проектов для Берляндии не редкость, однако оказалось, что и этих денег не хватило! Выяснилось, что в некоторый день i > 0 стоимость некоторого объекта j дополнительно повысилась на пока не известную следователям сумму X (то есть \(S_{i,j}\) = \(\sum_{m=1}^{j} S_{i-1,m}\) + X), что повлияло на стоимости объектов в последующие дни. Следователи выяснили, что из-за этого сумма итоговых стоимостей всех объектов увеличилась на \(R\) бурлей.
Помогите следователям выяснить минимально возможное значение X.
Входные данные
В первой строке входного файла содержатся три целых числа \(N\), \(K\), \(R\): количество олимпийских объектов (\(1 \le N \le 10^5\) ), количество дней увеличения стоимости объектов (\(1 \le K \le 10^5\) ) и количество бурлей, на которое незаконно возросла итоговая сумма (\(1 \le R \le 10^{18}\)). В следующей строке входного файла содержатся N целых чисел \(a_i\) — стоимости объектов в нулевой день (\(1 \le a_i \le 10^9\)).
Выходные данные
Единственная строка выходного файла должна содержать единственное целое число — минимально возможное значение \(X\)
Система оценки
Тесты к этой задаче состоят из четырех групп.
0. Тест 1. Тест из условия, оцениваемый в ноль баллов.
1. Тесты 2—25. В тестах этой группы \(N \le 10, K \le 10, a_i \le 10\), искомое значение \(X\) не превосходит \(10\). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы.
2. Тесты 26—38. В тестах этой группы \(N \le 1 000, K \le 1 000\). Эта группа оценивается в 30 баллов, баллы начисляются только при прохождении всех тестов группы. Решение будет тестироваться на тестах этой группы только в случае прохождения всех тестов первой группы.
3. В тестах этой группы дополнительные ограничения отсутствуют. Эта группа оценивается в 40 баллов. Тесты в этой группе оцениваются \t{независимо}
Примеры
Входные данные
3 3 12 1 3 3
Выходные данные
2
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Компания RectanGas занимается добычей нефти уже с незапяматных времен и является бесспорным лидером в своей области. Маркетологи считают, что она стала такой успешной благодаря бессменному исполнительному директору. На нем стоит остановиться поподробнее.
Дело в том, что исполнительный директор совсем не изучал геометрию в школе и до сих пор считает, что кроме прямоугольников других геометрических фигур не существует. Более того, он никак не может поверить, что стороны прямоугольников могут быть не параллельными осям координат. Поэтому все нефтяные вышки строятся следующим образом: директор на карте отмечает четыре точки так, чтобы они образовывали прямоугольник со сторонами, параллельными осям координат карты, и приказывает строить нефтяные вышки на участках, соответствующим отмеченным точкам на карте. Эти нефтяные вышки за короткий промежуток времени добывают всю нефть, расположенную на соответствующем участке.
Компания RectanGas почти выполнила свой план по добыче нефти на май 2010 года. Для этого ей осталось добыть ровно S баррелей нефти. Заметим, что больше добывать нельзя, иначе компанию обвинят в монополии. Меньше добывать тоже нельзя, потому что исполнительный директор, будучи человеком пунктуальным, очень огорчится, что повлечет за собой увольнение сотрудников и всеобщую безработицу. Геологи, подробно изучив карту местности, определили количество залежей нефти на каждом участке и попросили Вас написать программу, определяющую координаты будущих нефтяных вышек с учетом всех требований.
Входные данные
Первая строка содержит три числа: размеры карты местности n и m и план по добыче нефти S ( 2 ≤ n , m ≤ 300 ; 0 ≤ S ≤ 10 7 ). Далее следуют n строк по m чисел a ij — количество залежей нефти на соответсвующем участке ( 0 ≤ a ij ≤ 10 6 )
Выходные данные
В случае, если увольнения не миновать, выведите « - 1 » (без кавычек). В противном случае выведите четыре числа — координаты левой верхней и правой нижней вышек соответственно. Если вариантов ответа несколько, то выведите любой из них.
Примечание
Обратите внимание, в этой задаче TL равен 500 мс.
Иллюстрация к первому примеру:
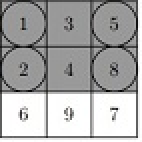
Сумма значений в угловых вышках равна 1 + 5 + 2 + 8 = 16
Примеры
Входные данные
3 3 16 1 3 5 2 4 8 6 9 7
Выходные данные
1 1 2 3
Входные данные
2 3 4 12 6 7 4 9 5
Выходные данные
-1
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Для моделирования различных объектов часто применяются так называемые клеточные поля. В простейшем случае – это прямоугольные таблицы, характеризующие некоторую область, а в каждой ячейке таблицы записывается какая-либо информация об исследуемом объекте. В биологии для моделирования распространения вирусов на плоской области в каждой ячейке помечается наличие вируса, а его распространение осуществляется в соседние ячейки по вертикали и горизонтали за одну единицу времени. Некоторые клетки обладают иммунитетом, заразить их невозможно и через них не распространяются вирусы.
Требуется написать программу, которая определяет минимально возможное число вирусов, с помощью которых можно заразить всю исследуемую прямоугольную область (за исключением защищённых клеток).
В приведённом примере таблица имеет размер \(4\times5\), в ней символом "I" помечены защищённые клетки. Видно, что двух вирусов достаточно для заражения всей области. Их можно поместить, например, в клетки, помеченные символом "V".
Входные данные
В первой входной строке записаны два натуральных числа \(M\) и \(N\) - размеры таблицы (количество строк и столбцов соответственно). Известно, что
\(1 \le M, N \le 100\). Во второй строке вначале записано одно число \(K\) - количество защищённых клеток, а далее записаны \(2K\) чисел – координаты этих клеток \(x_i\), \(y_i\) (\(0 \le k \le M \times N, 1 \le x_i \le M, 1 \le y_i \le N\)).
Выходные данные
Программа должна вывести одно число – минимально возможное число вирусов.
Примеры
Входные данные
4 5 3 1 3 2 1 2 2
Выходные данные
2
Выбрано
:
|