#1192

Соберите числа

Темы: [Эвристические методы]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2007, Лига А, Задача J ]

У Васи в распоряжении оказался набор кубиков. Вася решил на каждой грани каждого кубика написать по цифре и дальше использовать кубики для того, чтобы складывать из них числа. Вася хочет написать цифры так, чтобы уметь складывать любое число от 1 до некоторого числа K. Посчитайте такое максимальное K, до которого Вася сможет выкладывать все числа, если в распоряжении у Васи оказалось N кубиков. Заметьте, что если на какой-то грани какого-то кубика написана цифра 6, то эту же грань можно использовать и как цифру 9, просто перевернув соответствующий кубик.

При выкладывании числа Вася не обязан использовать все кубики. Ведущие нули в числах не нужны.

Рассмотрим примеры.

Пусть N=1. Тогда, написав на гранях кубика цифры от 1 до 6, Вася сможет выкладывать числа от 1 до 6. Тем самым, K=6.

Пусть N=2. Тогда, написав на гранях одного кубика цифры от 1 до 6, а на гранях другого цифры 0, 1, 2, 3, 7, 8, Вася сможет выложить любое число от 1 до 43.

Входные данные

Во входном файле записано одно число N (1≤N≤1000000).

Выходные данные

В выходной файл выведите максимальное значение K такое, что имея N кубиков Вася может так написать на их гранях цифры, чтобы было возможно выложить любое число от 1 до K.

Примеры

Входные данные

Выходные данные

Входные данные

Выходные данные

#1337

Компьютерная сеть

Темы: [Клеточная геометрия] [Обход в глубину] [Эвристические методы]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2009, Задача A ]

Для проведения олимпиады школьников по информатике требуется соединить компьютеры в сеть. Организаторы олимпиады разработали схему соединения компьютеров. В соответствии с этой схемой некоторые пары компьютеров должны быть соединены кабелем, и сигнал сможет дойти по кабелям от любого компьютера до любого другого, возможно, через другие компьютеры.

Некоторые компьютеры могут быть соединены циклически. Цикл называется простым, если каждый компьютер из этого цикла соединён ровно с двумя другими компьютерами этого цикла, и в этот цикл никакой кабель не входит более одного раза. Некоторые кабели могут не входить ни в какой цикл.

Известно, что в разработанной схеме никакой кабель не принадлежит двум простым циклам одновременно.

Организаторам олимпиады поручено разместить компьютеры в зале соревнований. При размещении должны выполняться следующие условия:

1.Компьютеры размещаются на плоскости в точках с целочисленными координатами.

2.Координаты компьютеров x и y лежат в диапазоне 0 ≤ x, y ≤ 10⁶.

3.Никакие два компьютера не располагаются в одной точке.

4.Кабели являются отрезками прямых.

5.Кабели не пересекаются между собой и не проходят через точки размещения компьютеров, к которым они не подключены.

Требуется написать программу, выполняющую размещение компьютеров по заданному описанию схемы.

Входные данные

В первой строке входного файла содержатся числа N и M — количество компьютеров и количество кабелей в схеме (1 ≤ N ≤ 100 000, 0 ≤ M ≤ 200 000). В последующих M строках содержатся пары чисел, разделенных пробелами. Каждая такая пара описывает один кабель, числа представляют собой номера соединенных компьютеров. Компьютеры пронумерованы от 1 до N. Никакая пара не встречается дважды, и никакой кабель не соединяет компьютер с самим собой.

Выходные данные

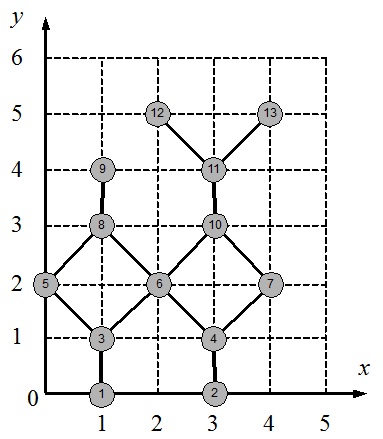
Выходной файл должен содержать N строк. Строка с номером i должна содержать координаты i-го компьютера, разделенные пробелом. Сначала выводится координата x, затем y. Разрешается вывести любой вариант размещения компьютеров, при котором выполняются условия 1–5.

Примечания

Решения, корректно работающие при отсутствии циклов, будут оцениваться из 40 баллов.

Решения, корректно работающие при наличии только одного цикла, будут оцениваться из 60 баллов.

Пример входных и выходных данных

Ввод

Вывод

13 14

11 12

11 13

1 3

3 5

5 8

8 9

8 6

6 3

4 6

4 2

6 10

10 11

10 7

7 4

1 0

3 0

1 1

3 1

0 2

2 2

4 2

1 3

1 4

3 3

3 4

2 5

4 5

#1616

Средняя зарплата

Темы: [Эвристические методы]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2009, Лига А, Задача A ]

В фирме MacroHard работают \(N\) сотрудников, каждый из которых получает зарплату, выражающуюся целым числом рублей. Известно, что ни один сотрудник не получает меньше 5000 рублей, и никто не получает больше 100000 рублей. Также известно, что средняя зарплата сотрудника в этой фирме выражается целым числом копеек и составляет \(A\) рублей \(B\) копеек.

Журналист, готовя публикацию об этой фирме, решил привести зарплаты всех сотрудников. Однако оказалось, что это коммерческая тайна. Журналиста это не смутило, и он решил придумать всем сотрудникам зарплаты. Однако у него возникла сложность – для правдоподобности должны выполняться все общеизвестные ограничения (зарплаты должны выражаться целым числом рублей из диапазона от 5000 до 100000, и вычисление средней зарплаты должно в точности приводить к результату \(A\) рублей \(B\) копеек).

Помогите ему! Напишите программу, которая по введенным числам \(N\), \(A\), \(B\) «придумает» и выведет \(N\) зарплат.

Входные данные

Вводятся натуральное число \(N\) (1 ≤ \(N\) ≤ 100), натуральное число \(A\) (10000 ≤ \(A\) ≤ 30000) и целое число \(B\) (0 ≤ \(B\) ≤ 99).

Выходные данные

Выведите \(N\) целых чисел, выражающих зарплаты сотрудников в рублях. Если возможных вариантов распределения зарплат несколько, выведите любой из них. Если распределить зарплаты с учетом наложенных условий невозможно, выведите одно число 0.

#1621

Язык Мумба-Юмба

Темы: [Эвристические методы] [Простые задачи на перебор]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2009, Лига А, Задача F ]

Слова в языке Мумба-Юмба могут состоять только из букв \(a\), \(b\) и при этом:

* никогда не содержат двух букв \(b\) подряд,
* ни в одном слове никогда не встречается три одинаковых подслова подряд. Например, по этому правилу в язык Мумба-Юмба не могут входить слова aaa (так как три раза подряд содержит подслово a), ababab (так как три раза подряд содержит подслово ab), aabababa (также три раза подряд содержит подслово ab).
Все слова, удовлетворяющие вышеописанным правилам, входят в язык Мумба-Юмба.
Напишите программу, которая подсчитает количество слов длины ровно \(K\) символов в языке племени Мумба-Юмба.

Входные данные

Вводится одно число \(K\) (1 ≤ \(K\) ≤ 100 000)

Выходные данные

Выведите одно число — количество слов в этом языке длины \(K\).

#1626

Средняя зарплата

Темы: [Эвристические методы]

Источники: [ Командные олимпиады, Московская командная олимпиада, 9-11 классы, 2009, Лига Б, Задача A ]

В фирме MacroHard работают \(N\) сотрудников, каждый из которых получает зарплату, выражающуюся целым числом рублей. Известно, что ни один сотрудник не получает меньше 5000 рублей, и никто не получает больше 100000 рублей. Также известно, что средняя зарплата сотрудника в этой фирме выражается целым числом копеек и составляет \(A\) рублей \(B\) копеек.
Журналист, готовя публикацию об этой фирме, решил привести зарплаты всех сотрудников. Однако оказалось, что это коммерческая тайна. Журналиста это не смутило, и он решил придумать всем сотрудникам зарплаты. Однако у него возникла сложность – для правдоподобности должны выполняться все общеизвестные ограничения (зарплаты должны выражаться целым числом рублей из диапазона от 5000 до 100000, и вычисление средней зарплаты должно в точности приводить к результату \(A\) рублей \(B\) копеек).
Помогите ему! Напишите программу, которая по введенным числам \(N\), \(A\), \(B\) «придумает» и выведет \(N\) зарплат. Гарантируется, что решение существует.

Входные данные

Вводятся натуральное число \(N\) (1 ≤ \(N\) ≤ 100), натуральное число \(A\) (10000 ≤ \(A\) ≤ 30000) и целое число \(B\) (0 ≤ \(B\) ≤ 99).

Выходные данные

Выведите \(N\) целых чисел, выражающих зарплаты сотрудников в рублях. Если возможных вариантов распределения зарплат несколько, выведите любой из них.

Примеры

Входные данные

5 10000 0

Выходные данные

10000 10000 10000 10000 10000