Андрей работает судьей на чемпионате по гипершашкам. В каждой игре в гипершашки участвует три игрока. По ходу игры каждый из игроков набирает некоторое положительное целое число баллов. Если после окончания игры первый игрок набрал \(a\) баллов, второй — \(b\), а третий \(c\), то говорят, что игра закончилась со счетом \(a:b:c\).
Андрей знает, что правила игры гипершашек устроены таким образом, что в результате игры баллы любых двух игроков различаются не более чем в \(k\) раз.
После матча Андрей показывает его результат, размещая три карточки с очками игроков на специальном табло. Для этого у него есть набор из n карточек, на которых написаны числа \(x_1, x_2, …, x_n\). Чтобы выяснить, насколько он готов к чемпионату, Андрей хочет понять, сколько различных вариантов счета он сможет показать на табло, используя имеющиеся карточки.
Требуется написать программу, которая по числу \(k\) и значениям чисел на карточках, которые имеются у Андрея, определяет количество различных вариантов счета, которые Андрей может показать на табло.
Первая строка входного файла содержит два целых числа: \(n\) и \(k (3 \le n \le 100 000, 1 \le k \le 10^9\) ).
Вторая строка входного файла содержит \(n\) целых чисел \(x_1, x_2, …, x_n (1 \le x_i \le 10^9 )\).
Выходной файл должен содержать одно целое число — искомое количество различных вариантов счета.
В приведенном примере Андрей сможет показать следующие варианты счета: 1:1:2, 1:2:1, 2:1:1, 1:2:2, 2:1:2, 2:2:1, 2:2:3, 2:3:2, 3:2:2. Другие тройки чисел, которые можно составить с использованием имеющихся карточек, не удовлетворяют заданному условию, что баллы любых двух игроков различаются не более чем в \(k\) = 2 раза.
В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.
\(3 \le n \le 100 000, k = 1, 1 \le x_i \le 100 000\)
\(3 \le n \le 100, k \le 100, 1 \le x_i \le 100\)
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\), все \(x_i\) различны
\(3 \le n \le 100 000, k \le 10^9 \le x_i \le 10^9\)
5 2 1 1 2 2 3
9
Совсем скоро начнётся чемпионат Хорватии по хорватскому хоккею. В хорватском хоккее каждая игра длится по M минут и в каждый момент времени на поле находятся ровно 6 игроков. Так как игра может длиться очень долго, не все игроки могут находится на поле на протяжении всей игры. Поэтому каждая команда привезла на чемпионат большое число запасных игроков.
Сегодня мы будем помогать Анте, тренеру команды Загреба. Анте привёз N игроков на чемпионат, причём у каждого игрока есть своя сила p i и своя выносливость d i . Для каждого игрока известно, что его «суммарное игровое время» не превышает величину его выносливости. «Суммарное игровое время» игрока — это суммарное количество времени, которое игрок провёл на поле. То есть, если игрок сначала провёл на поле X минут, а потом Y минут, то его «суммарное игровое время» равно X + Y минут.
В каждой момент времени у команды есть её сила — сумма сил всех шестерых игроков, находящихся на поле. Общая сила команды Z — это сумма сил команды во все минуты игры. То есть, если игра длилась 3 минуты и в первую минуту сила команды была 15 , во вторую — 12 , а в третью — 14 , то общая сила команды — 15 + 12 + 14 = 41 . Анте знает, что чтобы победить, надо максимизировать общую силу команды. Но Анте — не очень талантливый тренер, поэтому он просит вас помочь ему составить оптимальное расписание выхода команд, чтобы Z было максимально. Гарантируестя, что можно составить расписание так, чтобы в каждый момент на поле было по 6 игроков.
Обратите внимание, что в хорватском хоккее все игроки могут заменять друг друга, и вратаря нет, ведь так игра становиться гораздо веселее.
В первой строке вводится 2 числа M и N ( 1 ≤ M ≤ 5·10 5 , 6 ≤ N ≤ 5·10 5 ) — длительность матча в минутах и число игроков у команды соответственно.
В каждой из следующих N строк даны по 2 числа p i и d i ( 1 ≤ p i ≤ 10 5 , 1 ≤ d i ≤ M ) — сила и выносливость i -го игрока.
Все игроки пронумерованы от 1 до N в порядке, данном во входных данных.
В первой строке выведите Z — максимальную возможную общую силу команды.
Во второй строке выведите 6 чисел — номера игроков, которые должны выйти на поле с самого начала.
В третей строке выведите B — число замен. Обратите внимание, что число замен не должно превосходить 3· N .
В следующих B строках выведите по 3 числа X , Y , Z ( 1 ≤ X < M , 1 ≤ Y , Z ≤ N ), описывающие замену игрока Y на игрока Z в момент времени X . Обратите внимание, что можно проводить несколько замен в один момент времени, но не допускается выход в игру на нулевое время (т.е. выход в игру и замена в один момент времени или наоборот).
Если существует несколько ответов, выведите любой.
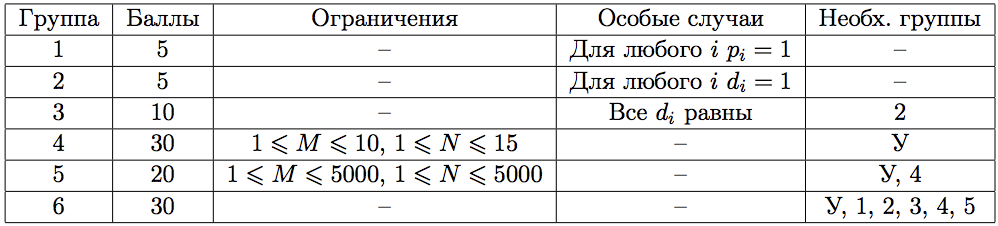
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, что прохождение тестов из условия (обозначается «У») не всегда обязательно для принятия на проверку.
200 6 3 200 4 200 5 200 6 200 7 200 8 200
6600 6 5 4 3 2 1 0
9 9 10 3 9 3 13 9 5 3 15 9 100 9 3 6 2 6 1 6
1260 6 5 3 1 7 8 4 3 8 9 3 1 2 6 7 8 6 2 4
3 9 100 3 100 3 100 3 100 3 100 2 100 1 50 1 30 2 1 1
1610 1 2 3 4 5 7 2 1 7 8 2 5 6