Мальчик Костя очень любит конфеты, но мама не разрешает ему брать их слишком много. Поэтому каждый раз, когда Костя хочет съесть конфету, мама предлагает ему сыграть в игру.
Изначально у Кости нет конфет, а у мамы их \(N\) (они пронумерованы от 1 до \(N\)). На каждой конфете мама написала два числа \(A_i\) и \(C_i\). Мама очень следит за уровеня вредности конфет, который получает ее сын. Изначально этот уровень равен 0. На каждом ходу игры Костя может взять одну конфету. Если Костя возьмет конфету с номером \(i\), то уровеня вредности увеличивается на \(A_i\). Если сразу после этого уровеня вредности становится большей \(C_i\), то брать эту конфету запрещается.
Брать конфеты можно в произвольном порядке, но одну и ту же можно брать не более одного раза.
Помогите Косте взять как можно больше конфет (вне зависимости от финального уровеня вредности).
В первой сроке входных данных записано целое число \(N\) (\(1 \le N \le 1000\)) \(-\) количество видов конфет. Во второй строке записаны \(N\) целых чисел \(A_i\) (\(1 \le A_i \le 10^6\)). В третей строке записаны \(N\) целых чисел \(C_i\) (\(1 \le C_i \le 10^9\)).
В единственной строке выведите целое число, равное максимальному количеству конфет, которые может взять Костя.
Теплым весенним днем группа из \(N\) школьников-программистов гуляла в окрестностях города Кисловодска. К несчастью, они набрели на большую и довольно глубокую яму. Как это случилось — непонятно, но вся компания оказалась в этой яме.
Глубина ямы равна \(H\). Каждый школьник знает свой рост по плечи \(h_i\) и длину своих рук \(l_i\). Таким образом, если он, стоя на дне ямы, поднимет руки, то его ладони окажутся на высоте \(h_i + l_i\) от уровня дна ямы. Школьники могут, вставая друг другу на плечи, образовывать вертикальную колонну. При этом любой школьник может встать на плечи любого другого школьника. Если под школьником \(i\) стоят школьники \(j_1, j_2, \ldots, j_k\), то он может дотянуться до уровня \(h_{j1} + h_{j2} + \ldots + h_{jk} + h_i + l_i\).
Если школьник может дотянуться до края ямы (то есть \(h_{j1} + h_{j2} + \ldots + h_{jk} + h_i + l_i \geq H\)), то он может выбраться из нее. Выбравшиеся из ямы школьники не могут помочь оставшимся.
Найдите наибольшее количество школьников, которые смогут выбраться из ямы до прибытия помощи, и перечислите их номера.
В первой строке входного файла записано натуральное число \(N\) — количество школьников, попавших в яму.
Далее в \(N\) строках указаны по два целых числа: рост \(i\)-го школьника по плечи \(h_i\) и длина его рук \(l_i\).
В последней строке указано целое число — глубина ямы \(H\).
В первой строке выведите \(K\) — максимальное количество школьников, которые смогут выбраться из ямы. Если \(K > 0\), то во второй строке выведите их номера в том порядке, в котором они вылезают из ямы. Школьники нумеруются с единицы в том порядке, в котором они заданы во входном файле. Если существует несколько решений, выведите любое.
Подзадача 1 (30 баллов) \(n \le 2\,000\) и \(1 \le l_i, h_i, H \le 1\,000\)
Подзадача 2 (40 баллов) \(n \le 2\,000\) и \(1 \le l_i, h_i, H \le 10^5\)
Подзадача 3 (30 баллов) \(n \le 100\,000\) и \(1 \le l_i, h_i, H \le 10^9\)
2 10 4 5 2 20
0
6 6 7 3 1 8 5 8 5 4 2 10 5 30
4 2 5 1 3
У Васи в комнате очень много коробок, которые валяются в разных местах. Васина мама хочет, чтобы он прибрался. Свободного места в комнате мало и поэтому Вася решил собрать все коробки и составить их одну на другую.
К сожалению, это может быть невозможно. Например, если на картонную коробку с елочными украшениями положить что-то железное и тяжелое, то вероятно следующий Новый год придется встречать с новыми игрушками.
Вася взвесил каждую коробку и оценил максимальный вес который она может выдержать. Помогите ему определить какое наибольшее количество коробок \(m\) он сможет составить одну на другую так, чтобы для каждой коробки было верно, что суммарный вес коробок сверху не превышает максимальный вес, который она может выдержать.
Первая строка входного файла содержит целое число \(n\) (\(1 \le n \le 10^5\)) - количество коробок в комнате. Каждая следующая из \(n\) строк содержит два целых числа \(w_i\) и \(c_i\) (\(1 \le w_i \le 10^5, 1 \le c_i \le 10^9\)), где \(w_i\) \(-\) это вес коробки с номером \(i\), а \(c_i\) \(-\) это вес который она может выдержать.
В выходной файл выведите одно число \(-\) ответ на задачу.
1 ≤ n ≤ 1 250. Решение оценивается в 50 баллов.
Дополнительные ограничения отсутствуют. Решение оценивается в 50 баллов.
3 10 11 20 100 30 10
3
3 11 11 20 100 30 10
2
Есть N шариков, висящих в воздухе вдоль одной линии слева направо. Девочка Перика хочет поиграть со стрелами и проверить свои навыки охотника. Она стреляет в линию шариков слева, запуская стрелу на некоторой высот. Стрела летит вдоль линии слева направо до тех пор, пока не попадет в шарик. В тот момент, когда она его касается, шарик лопается, а стрела летит дальше на высоте, уменьшенной на 1. То есть, если стрела летела на высоте H , то после столкновения она будет лететь на высоте H - 1 . Цель нашего героя - сбить все шарики, использовав минимальное количество стрел.
В первой строке записано одно натуральное число N ( 1 ≤ N ≤ 1000000 ). Во второй строке записано N натуральных чисел H i . Каждое число H i ( 1 ≤ H i ≤ 1000000 ) обозначает высоту, на которой висит i-й шарик в порядке слева направо.
В единственной строке выведите одно целое число - минимальное количество выстрелов, необходимое Перике для того чтобы сбить все шарики.
5 2 1 5 4 3
2
5 1 2 3 4 5
5
5 4 5 2 1 4
3
Совсем скоро начнётся чемпионат Хорватии по хорватскому хоккею. В хорватском хоккее каждая игра длится по M минут и в каждый момент времени на поле находятся ровно 6 игроков. Так как игра может длиться очень долго, не все игроки могут находится на поле на протяжении всей игры. Поэтому каждая команда привезла на чемпионат большое число запасных игроков.
Сегодня мы будем помогать Анте, тренеру команды Загреба. Анте привёз N игроков на чемпионат, причём у каждого игрока есть своя сила p i и своя выносливость d i . Для каждого игрока известно, что его «суммарное игровое время» не превышает величину его выносливости. «Суммарное игровое время» игрока — это суммарное количество времени, которое игрок провёл на поле. То есть, если игрок сначала провёл на поле X минут, а потом Y минут, то его «суммарное игровое время» равно X + Y минут.
В каждой момент времени у команды есть её сила — сумма сил всех шестерых игроков, находящихся на поле. Общая сила команды Z — это сумма сил команды во все минуты игры. То есть, если игра длилась 3 минуты и в первую минуту сила команды была 15 , во вторую — 12 , а в третью — 14 , то общая сила команды — 15 + 12 + 14 = 41 . Анте знает, что чтобы победить, надо максимизировать общую силу команды. Но Анте — не очень талантливый тренер, поэтому он просит вас помочь ему составить оптимальное расписание выхода команд, чтобы Z было максимально. Гарантируестя, что можно составить расписание так, чтобы в каждый момент на поле было по 6 игроков.
Обратите внимание, что в хорватском хоккее все игроки могут заменять друг друга, и вратаря нет, ведь так игра становиться гораздо веселее.
В первой строке вводится 2 числа M и N ( 1 ≤ M ≤ 5·10 5 , 6 ≤ N ≤ 5·10 5 ) — длительность матча в минутах и число игроков у команды соответственно.
В каждой из следующих N строк даны по 2 числа p i и d i ( 1 ≤ p i ≤ 10 5 , 1 ≤ d i ≤ M ) — сила и выносливость i -го игрока.
Все игроки пронумерованы от 1 до N в порядке, данном во входных данных.
В первой строке выведите Z — максимальную возможную общую силу команды.
Во второй строке выведите 6 чисел — номера игроков, которые должны выйти на поле с самого начала.
В третей строке выведите B — число замен. Обратите внимание, что число замен не должно превосходить 3· N .
В следующих B строках выведите по 3 числа X , Y , Z ( 1 ≤ X < M , 1 ≤ Y , Z ≤ N ), описывающие замену игрока Y на игрока Z в момент времени X . Обратите внимание, что можно проводить несколько замен в один момент времени, но не допускается выход в игру на нулевое время (т.е. выход в игру и замена в один момент времени или наоборот).
Если существует несколько ответов, выведите любой.
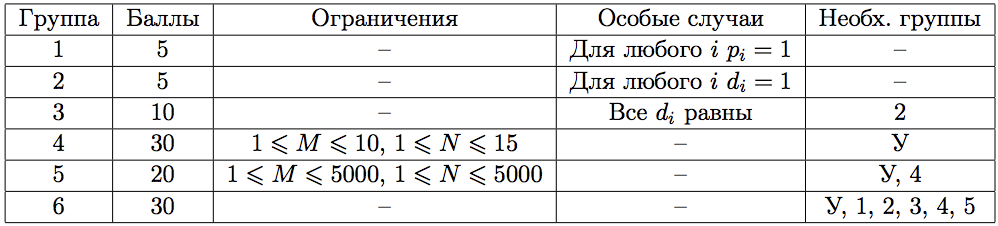
Тесты к этой задаче состоят из трёх групп. Баллы за каждую группу ставятся только при прохождении всех тестов группы и всех тестов некоторых из предыдущих групп. Обратите внимание, что прохождение тестов из условия (обозначается «У») не всегда обязательно для принятия на проверку.
200 6 3 200 4 200 5 200 6 200 7 200 8 200
6600 6 5 4 3 2 1 0
9 9 10 3 9 3 13 9 5 3 15 9 100 9 3 6 2 6 1 6
1260 6 5 3 1 7 8 4 3 8 9 3 1 2 6 7 8 6 2 4
3 9 100 3 100 3 100 3 100 3 100 2 100 1 50 1 30 2 1 1
1610 1 2 3 4 5 7 2 1 7 8 2 5 6