Митя знаком с \(m\) юношами и \(n\) девушками и хочет пригласить часть из них на свой день рождения. Ему известно, с какими девушками знаком каждый юноша, и с какими юношами знакома каждая девушка. Он хочет добиться того, чтобы каждый приглашённый был знаком со всеми приглашёнными противоположного пола, пригласив при этом максимально возможное число своих знакомых.
Входной файл состоит из одного или нескольких наборов входных данных. В первой строке входного файла записано число наборов \(k\) (\(1\le k\le 20\)). В последующих строках записаны сами наборы входных данных. В первой строке каждого набора задаются числа \(0\le m\le 150\) и \(0\le n\le 150\). Далее следуют \(m\) строк, в каждой из которых записано одно или несколько чисел — номера девушек, с которыми знаком \(i\)-й юноша (каждый номер встречается не более одного раза). Строка завершается числом 0.
Для каждого набора выведите четыре строки. В первой из них выведите максимальное число знакомых, которых сможет пригласить Митя. В следующей строке выведите количество юношей и количество девушек в максимальном наборе знакомых. Следующие две строки должны содержать номера приглашённых юношей и приглашённых девушек соответственно. Если максимальных наборов несколько, то выведите любой из них.
2 2 2 1 2 0 1 2 0 3 2 1 2 0 2 0 1 2 0
4 2 2 1 2 1 2 4 2 2 1 3 1 2
Недавно на уроке во время контрольной Мария Ивановна перехватила записку Саше от Оли. Мария Ивановна очень хочет знать, что в записке, но, к сожалению, записка зашифрована. Мария Ивановна знает, что её ученики для шифровки заменяют каждую букву исходного сообщения на какую-то другую. Замена происходит таким образом, что одинаковые буквы всегда заменяются одной и той же буквой, а разные — разными.
Мария Ивановна подозревает, что записка — это ответы к контрольному тесту (ведь её длина случайно оказалась равной длине строки с правильными ответами). Однако она знает, что ответы Оли не обязательно полностью правильны. На каждый вопрос возможен один из K вариантов ответа. Естественно, Мария Ивановна знает правильные ответы.
Мария Ивановна решила расшифровать записку таким способом, чтобы максимизировать количество правильных ответов Оли. Однако, она очень занята, поэтому попросила Вас помочь ей в этом пустяковом деле.
В первой строке задана длина каждой из строк N (1 ≤ N ≤ 2 000 000) и K — количество возможных ответов на каждый вопрос (1 ≤ K ≤ 52). Ответы нумеруются в порядке abcde...xyzABCDE...XYZ. То есть, при K = 6 возможные ответы выглядят как abcdef, а при K = 30 "— abcde...xyzABCD.
Во второй строке задана зашифрованная записка — строка, состоящая из строчных и заглавных латинских букв.
В третьей строке заданы правильные ответы — строка той же длины, что и первая, состоящая из строчных и заглавных латинских букв.
В первой строке выведите единственное число — максимально возможное количество правильных ответов у Оли.
Во второй строке выведите расшифровку — строчку длины K, где по порядку для каждой буквы из шифра учеников указано, какому ответу она соответствует.
Если несколько расшифровок дают правильный ответ, выведите любую.
Тесты к этой задаче состоят из четырех групп.
- Тесты 1-3. Тесты из условия, оцениваются в ноль баллов.
- Тесты 4-15. В тестах этой группы K = 2. Решение оценивается в 15 баллов.
- Тесты 16-40. В тестах этой группы K ≤ 9. Решение оценивается в 15 баллов.
- Тесты 41-75. В тестах этой группы K ≤ 26. Решение оценивается в 30 баллов.
- Тесты 76-115. Дополнительные ограничения отсутствуют. Решение будет тестироваться на тестах этой группы только в случае прохождения всех предыдущих групп. Группа оценивается в 40 баллов.
Баллы за каждую группу тестов ставятся только при прохождении всех тестов группы. Тестирование на очередной группе начинается только после полного прохождения предыдущей.
10 2 aaabbbaaab bbbbabbbbb
7 ba
10 2 aaaaaaabbb bbbbaaabbb
6 ab
9 4 dacbdacbd acbdacbda
9 cdba
Вася очень любит различные игры: шашки, шахматы, домино, крестики-нолики и т. д. Поскольку он играет в них уже достаточно давно, он успел изучить эти игры достаточно хорошо, и они стали скучными. Поэтому он теперь изобретает новые игры на основе тех, в которые уже наигрался. Недавно он изобрел игру «Доминошахматы».
Она состоит в следующем: Вася берет у дедушки большой кусок фанеры и раскрашивает его так, что у него получается шахматная доска размера N × M клеточек. Потом он берет кости домино и пытается покрыть ими полученную доску так, чтобы все клеточки были закрыты, не было наложений и никакие доминошки не торчали за края доски (каждая доминошка покрывает две соседние клетки).
Поскольку Вася не спрашивает разрешения у дедушки прежде, чем взять доску, он иногда берет ненужные доски, а иногда и те, которые дедушка хотел использовать в строительстве новой дачи. Как раз сегодня Вася взял «нужную» доску, поэтому дедушка был вынужден вырезать из Васиной доски два квадрата по одной клеточке.
Вася сначала огорчился, что не сможет поиграть в свою игру. А потом решил попробовать замостить доску с уже вырезанными клетками, причем так, чтобы вырезанные клетки не были накрыты доминошками.
Помогите Васе понять, можно ли это сделать.
В первой строке входных данных записаны числа N и M — размеры доски (1 ≤ N ≤ 200, 1 ≤ M ≤ 200, N·M > 2).
Во второй строке вводятся через пробел два целых числа — координаты x1 и y1 первой вырезанной клетки (1 ≤ x1 ≤ N, 1 ≤ y1 ≤ M).
В третьей строке вводятся через пробел два целых числа — координаты x2 и y2 второй вырезанной клетки (1 ≤ x2 ≤ N, 1 ≤ y2 ≤ M).
Первая и вторая клетки не совпадают.
Выведите «YES», если доску с вырезанными клеточками можно покрыть доминошками, и «NO» в противном случае. (Запас доминошек у Васи бесконечный.)
2 2 1 1 2 2
NO
2 2 1 1 1 2
YES
Женя недавно купил себе новую соковыжималку. Теперь по утрам он и его братья и сестры пьют свежевыжатый фруктовый сок. А это, между прочим, очень полезно!
Недавно они поняли, что можно пить сок, выжатый не только из одного вида фруктов, как, например, апельсиновый, но и различные смеси, например, виноградно-яблочный.
В Жениной семье все очень любят сок, поэтому могут утром выпить не один стакан, причем разных видов сока. Например, его сестра Катя очень любит грейпфрутовый и апельсиновый соки. Женя, как наиболее технически грамотный человек, каждое утро занимается приготовлением соков.
Опишем подробнее, как работает соковыжималка. В нее загружаются фрукты, они проходят отжим в центрифуге, обезвоженная мякоть сбрасывается в отдельный резервуар, а сок попадает в специальную емкость.
Основная проблема состоит в том, что эту емкость иногда приходится мыть. Например, если после приготовления апельсинового сока, необходимо приготовить яблочный, то емкость надо мыть, иначе получится апельсиново-яблочный сок. Более формально, пусть сок A состоит из компонентов a1, ..., an, а сок B из компонентов b1, ..., bm. Сок B можно готовить после сока A, если любой из компонентов ai является компонентом сока B (т.е.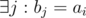 
). В противном случае емкость для сока надо помыть.
Женя не очень любит мыть посуду, поэтому хочет мыть емкость как можно меньшее число раз. Помогите ему.
Первая строка входного файла содержит количество N различных соков, которые требуется приготовить (1 ≤ N ≤ 300). Каждая из последующих N строк описывает один из соков. Описание сока состоит из числа k его компонентов (1 ≤ k ≤ 300) и списка этих компонентов. Каждый из компонентов сока описывается словом длиной до 30 символов из строчных и прописных букв латинского алфавита. Прописные и строчные буквы различаются. Различные компоненты имеют различные названия.
В выходной файл выведите минимальное количество раз, которое Жене придется помыть емкость для сока. Учитывайте при этом, что емкость для сока надо помыть и после приготовления последней порции сока.
4 1 Apple 2 Apple Orange 1 Orange 2 Orange Pineapple
2
3 1 Apple 1 Orange 1 Mango
3
Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами (Xi, Yi) декартовыми координатами.
Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке (X1, Y1) и завешает его вместе с хозяином в точке (XN, YN).
Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел (X'j, Y'j). Всего таких мест M. Тем не менее, покидая своего хозяина в точке (Xi, Yi) (где 1 ≤ i ≤ N), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке (Xi + 1, Yi + 1).
Ваша задача найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки (Xi, Yi) и посещенные интересные места (X'j, Y'j). Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.
Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:
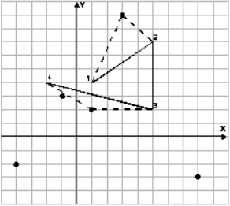
На первой строке через пробел записаны два числа N и M (2 ≤ N ≤ 100, 0 ≤ M ≤ 100). Вторая строка содержит N пар целых чисел X1, Y1, ..., XN, YN, разделенных пробелом, описывающих путь Боба. В третьей строке записано M пар целых чисел, (X'1, Y'1), ... (X'M, Y'M), разделенных пробелом, описывающих интересные места.
Все точки в условии различны и координаты по модулю не превосходят 1000.
В выходном файле должно быть единственное число K количество вершин в оптимальном маршруте Ральфа.
4 5 1 4 5 7 5 2 -2 4 -4 -2 3 9 1 2 -1 3 8 -3
6