Охотник Боб часто гуляет со своей собакой Ральфом. Боб гуляет с постоянной скоростью и его путь – ломаная (возможно, самопересекающаяся), каждая вершина которой задается двумя целыми числами ( X i , Y i ) – декартовыми координатами.
Ральф бегает сам по себе, но обязательно должен встречаться с хозяином в указанных N точках. Собака начинает свой путь одновременно с хозяином в точке ( X 1 , Y 1 ) и завешает его вместе с хозяином в точке ( X N , Y N ) .
Ральф может бегать с любой скоростью, не превышающей в два раза скорость Боба. Пока Боб идет по прямой из точки в точку, собака ищет деревья, кусты, холмики и прочие интересные места, которые заданы парами целых чисел ( X ' j , Y ' j ) . Всего таких мест M. Тем не менее, покидая своего хозяина в точке ( X i , Y i ) (где 1 ≤ i ≤ N ), Ральф посещает не более одного интересного места перед тем, как опять встретить хозяина в точке ( X i + 1 , Y i + 1 ) .
Ваша задача – найти маршрут, удовлетворяющий указанным выше условиям, с максимальным количеством посещаемых интересных мест. Он представляется ломаной, по которой бегает Ральф. Ее вершинами должны быть все точки ( X i , Y i ) и посещенные интересные места ( X ' j , Y ' j ) . Последние должны быть посещены (то есть встречаться в описании пути) не более одного раза.
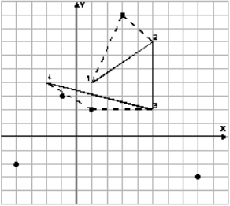
Пример пути Боба (сплошная линия), набора интересных мест (точки) и одного из лучших путей Ральфа представлены на рисунке:
На первой строке через пробел записаны два числа N и M (2 ≤ N ≤ 100, 0 ≤ M ≤ 100) . Вторая строка содержит N пар целых чисел X 1 , Y 1 , ..., X N , Y N , разделенных пробелом, описывающих путь Боба. В третьей строке записано M пар целых чисел, ( X ' 1 , Y ' 1 ) , ... ( X ' M , Y ' M ) , разделенных пробелом, описывающих интересные места.
Все точки в условии различны и координаты по модулю не превосходят 1000 .
В выходном файле должно быть единственное число K – количество вершин в оптимальном маршруте Ральфа.
4 5 1 4 5 7 5 2 -2 4 -4 -2 3 9 1 2 -1 3 8 -3
6
В маленьком городке М начала действовать служба контроля за незаконными полетами НЛО. Первая задача службы — выяснить, сколько НЛО действует в окрестности города. Агенты службы опросили множество свидетелей и составили список случаев встречи с НЛО, произошедших за одни сутки, с указанием места и времени наблюдения. Теперь аналитики хотят понять, сколько же на самом деле было НЛО. Из данных разведки известна максимальная скорость, с которой может лететь НЛО. Аналитики просят вас узнать, какое минимальное количество НЛО могли наблюдать свидетели.
На первой строке входного файла содержатся целые числа n и v — количество случаев наблюдения и максимальная скорость НЛО ( 1 ≤ n ≤ 100 , 1 ≤ v ≤ 10000 ). Следующие n строк содержат описания случаев встречи с НЛО в формате «ЧЧ:ММ x y», где ЧЧ:ММ — время встречи, x и y — координаты места, в котором наблюдался НЛО (для простоты будем считать, что все встречи происходили на плоскости). Координаты по модулю не превышают 1000 . Скорость выражена в км/ч, координаты — в км.
Выведите в выходной файл одно число — минимальное возможное количество НЛО.
4 1 12:00 0 0 13:10 0 1 14:00 1 0 15:00 1 1
2
На одной из планет, под названием TheBestWorld, живут много умных людей. Эта планета также известна своими двумя конкурирующими школами супергероев. Каждый малыш, живущий на этой планете, мечтает стать супергероем, но не у всех это получается.
Ученики разных школ всегда недолюбливали друг друга. И иногда дело даже доходило до того, как супергерои начали применять свои геройские силы для выяснения отношений.
В этом мире случилось несчастье. На TheBestWorld нападают темные силы. У генерала главнокомандующего армией супергероев есть в распоряжении n + m супергероев, из них n — выпускники первой школы, m — второй. Главнокомандующий подсчитал количество супергероев k , которые смогут спасти лучшее, что у них есть, — планету.
На первый взгляд кажется, что главнокомандующему не понадобится помощь в выборе супергероев, но он вспомнил, что супергерои из разных школ раздражают друг друга. Но это происходит только тогда, когда два супергероя из разных школ находятся на расстоянии меньше d . Если такую пару героев позвать спасать мир, они не смогут продуктивно делать свою работу.
Проблема в том, что генерал забыл искомое d . Вам известны координаты каждого из супергероев. Генерал просит вас вычислить максимальное d , при котором он все еще может спасти мир. И выдать список супергероев, которые спасут мир при данном d .
В первой строке входного файла заданы три числа n , m и k ( 1 ≤ k , n , m ≤ n + m ≤ 200 ) — количество супергероев, выпустившихся из первой и второй школы, и количество супергероев, которое необходимо, чтобы спасти мир, соответственно. Следующие n + m строк описывают супергероев: в каждой строке заданы два целых числа — текущие координаты супергероя. Первые n строк содержат информацию о выпускниках первой школы, следующие m — о выпускниках второй школы. Все координаты не превышает по модулю 10000 . Известно, что никакие два супергероя не стоят в одной точке.
В первую строку выходного файла выведите одно вещественное число: максимальное значение d , которое позволяет спасти мир, либо -1, если при любом значении d мир можно спасти. Относительная или абсолютная погрешность вашего ответа не должна превышать 10 −6 . В следующих k строках выведите список номеров супергероев по одному числу в строке, которых можно взять при данном d , либо, если спасти мир можно при любом d , выведите список героев, которые позволяет спасти мир вне зависимости от d . Супергерои нумеруются числами от 1 до n + m в том порядке, в котором они идут во входном файле.
2 3 4 1 1 1 2 1 3 1 4 1 5
2.000000000000000000 1 3 4 5
1 1 2 1 1 1 10
9.000000000000000000 1 2
В секретном 240 отделе ИПФ РАН \(N\) сотрудников и \(N\) компьютеров. В отделе вводятся новые требования к секретности. В соответствии с этими требованиями, для каждого сотрудника будут определены ровно \(K\) компьютеров, к которым этот сотрудник будет иметь допуск (т.е. за которыми этот сотрудник будет иметь право работать), причём так, что к каждому компьютеру будут иметь допуск ровно \(K\) сотрудников.
Информация о том, какой сотрудник к какому компьютеру будет иметь допуск, будет известна лишь непосредственно перед вступлением новых требований в силу. Таким образом, чтобы не прерывать работу отдела, сотрудники должны будут быстро решить, кто за каким компьютером будет работать. Для этого им необходимо заранее написать программу, которая по любому распределению допусков сотрудников найдёт рассадку сотрудников по компьютерам, удовлетворяющую этим допускам.
Обратите внимание, что значение \(K\) тоже будет известно лишь в последний момент. Из общих соображений секретности известно лишь, что \(K\) будет равняться или 1, или 2, или 4; поэтому ваша программа должна уметь работать для любого из этих трех значений \(K\).
Формат входных данных
В первой строке входного файла записаны натуральные числа \(N\) и \(K\) (\(1\leq N \leq 100 000\)). Далее следуют \(KN\) строк, в каждой из которых записаны два натуральных числа — номер сотрудника и номер компьютера, к которому этот сотрудник имеет допуск.
Гарантируется, что каждый сотрудник имеет допуск ровно к \(K\) компьютерам, что к каждому компьютеру ровно \(K\) сотрудников имеют допуск, и что \(K\) равно либо 1, либо 2, либо 4.
Формат выходных данных
В выходной файл выведите \(N\) строк, в каждой по два числа — номер сотрудника и номер компьютера, за которым он должен работать. Строки можно выводить в произвольном порядке.
Если есть несколько решений, выведите любое. Можно доказать, что для любого входного файла, удовлетворяющего указанным ограничениям, всегда имеется как минимум одно решение.
Примеры
| Ввод | Вывод |
|---|---|
3 1 2 3 3 1 1 2 |
3 1 1 2 2 3 |
2 2 1 2 2 1 2 2 1 1 |
1 2 2 1 |
Для каждой пары чисел \(x\) и \(y\) из диапазона \(0,1,2,\ldots,N-1\) определим расстояние \(D(x,y)\) как \(min(|x-y|,N-|x-y|)\). Для перестановки \(T\) можно построить набор чисел \(D_i=D(i,T_i)\). Ваша задача состоит в обратном: по заданному набору чисел восстановить корректную перестановку, а среди таких требуется выбрать лексикографически минимальную.
Формат входных данных
В первой строке входных данных содержится число \(N\) - размер перестановки. В следующей строке содержатся числа \(D_0,D_1,\ldots,D_{N-1}\).
Формат выходных данных
В случае, если такой перестановки не существует, выведите «No Answer». В противном случае выведите искомую оптимальную перестановку.
Система оценки
- В 30% тестовых примеров выполнено \(N \le 50\)
- В 60% тестовых примеров выполнено \(N \le 500\)
- В 100% тестовых примеров выполнено \(N \le 10\,000\)