--->
21 задач
<---
Источники
#868
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2008,
Лига Б,
Задача E
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Напишите программу, вычисляющую остаток от деления заданного «длинного» числа на заданную цифру.
Входные данные
В первой строке задана цифра K (1≤K≤9). Во второй строке задано натуральное число N, состоящее из не более чем 250 цифр.
Выходные данные
Выведите остаток от деления N на K.
Примеры
Входные данные | Выходные данные |
| 5 123456789 | 4 |
| 1 123 | 0 |
#872
Темы:
[Остатки]
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2008,
Лига Б,
Задача A
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
В часах села батарейка, и они стали идти вдвое медленнее. Когда на часах было x1 часов y1 минут, правильное время было a1 часов b1 минут. Сколько времени будет на самом деле, когда часы в следующий раз покажут x2 часов y2 минут.
Входные данные
Заданы числа x1, y1, a1, b1, x2, y2 в указанном порядке. Все числа целые. Числа x1, a1, x2 — от 0 до 23, числа y1, b1, y2 — от 0 до 59.
Выходные данные
Выведите два числа a2, b2, определяющие сколько будет времени на самом деле, когда на часах будет x2 часов y2 минут.
Примеры
Входные данные | Выходные данные |
| 12 34 10 34 12 35 | 10 36 |
| 12 34 10 0 2 34 | 14 0 |
#1340
Источники:
[
Личные олимпиады,
Всероссийская олимпиада школьников,
Заключительный этап,
2009,
Задача D
]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes
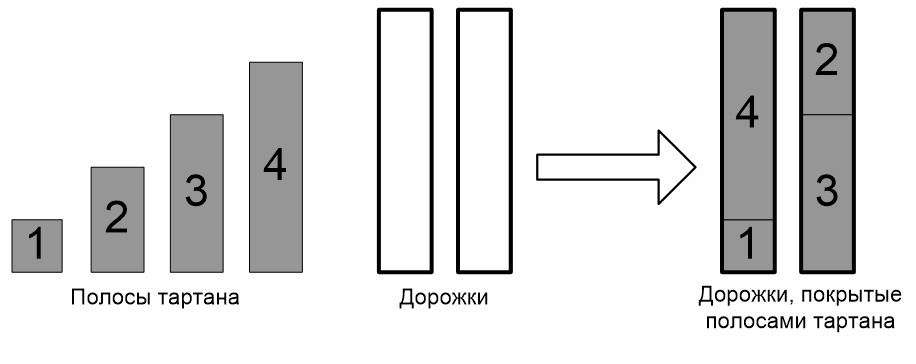
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).
Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.
Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.
Входные данные
Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).
Выходные данные
В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».
В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.
В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.
Примеры входных и выходных данных
| Ввод | Вывод |
| 2 4 | YES 2 1 4 2 3 2 |
| 3 4 | NO |
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Программист на Северном полюсе работал за компьютером в варежках и поэтому мог набирать только 0 и 1, а клавиша 0 запала. Сможет ли он набрать число, состоящее только из единиц и при этом кратное заданному N?
Входные данные
Программе дано число N (1 ≤ N ≤ 106).
Выходные данные
Вывести минимальное число, удволетворяющее требованию, или "NO" , если такого числа не существует.
Примеры
Входные данные
100
Выходные данные
NO
Входные данные
57
Выходные данные
111111111111111111
#1627
Темы:
[Остатки]
Источники:
[
Командные олимпиады,
Московская командная олимпиада,
9-11 классы,
2009,
Лига Б,
Задача B
]
ограничение по времени на тест
0.4 second;
ограничение по памяти на тест
64 megabytes
\(N\)-лягушка живет на болоте, на котором в ряд растут бесконечно много кувшинок, пронумерованных слева направо числами 1, 2, 3, ...
Изначально N-лягушка сидит на кувшинке с номером \(K\) (\(K\) > \(N\)). Каждый раз \(N\)-лягушка прыгает на \(N\) кувшинок влево и повторяет это, пока не оказывается на номере, меньше либо равном \(N\). Если она попадает на кувшинку с номером \(N\), то становится счастливой, и дальше никуда не прыгает. Если же она попадает на кувшинку с каким-нибудь номером \(M\) < \(N\), то огорчается, прыгает на \(N\) кувшинок вправо и превращается в \(M\)-лягушку (теперь она будет прыгать на \(M\) клеток влево и мечтать попасть на клетку номер \(M\), а если у нее это не получится, то она превратится в \(X\)-лягушку, и так далее).
Требуется выяснить, исполнятся ли когда-либо мечты \(N\)-лягушки, сидящей изначально на кувшинке с номером \(K\), и если да, то на какой кувшинке она окажется.
Входные данные
Вводятся два натуральных числа \(N\) и \(K\). 1 ≤ \(N\) < \(K\) ≤ 2∙\(10^9\).
Выходные данные
Выведите номер кувшинки, на которой останется \(N\)-лягушка. Если мечты лягушки никогда не исполнятся, выведите одно число 0.
Примеры
Входные данные
2 10
Выходные данные
2
Выбрано
:
|