--->
260 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Даны пять действительных чисел: \(x\), \(y\), \(x_c\), \(y_c\), \(r\).
Проверьте, принадлежит ли точка \((x,y)\) кругу с центром \((x_c,y_c)\)
и радиусом \(r\). Если точка принадлежит кругу, выведите слово YES,
иначе выведите слово NO.
Решение должно содержать функцию IsPointInCircle(x, y, xc, yc, r),
возвращающую True, если точка принадлежит кругу и False, если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию IsPointInCircle
и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInCircle не должна содержать инструкцию if.
Входные данные
Вводится пять действительных чисел.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
0.5 0.5 0 0 1
Выходные данные
YES
Входные данные
0.5 0.5 1 1 0.1
Выходные данные
NO
Проверьте, принадлежит ли точка данной закрашенной области:
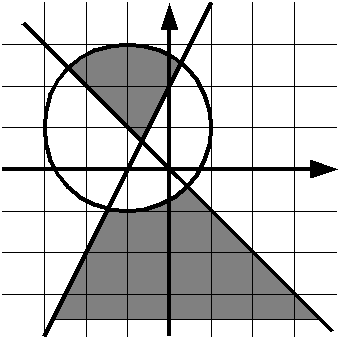
Если точка принадлежит области (область включает границы), выведите слово YES,
иначе выведите слово NO.
Решение должно содержать функцию IsPointInArea(x, y),
возвращающую True, если точка принадлежит области и False, если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию IsPointInArea
и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInArea не должна содержать инструкцию if.
Входные данные
Вводится два действительных числа.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
-2 1
Выходные данные
NO
Входные данные
-2 2
Выходные данные
YES
Дано действительное положительное число \(a\) и целоe число \(n\).
Вычислите \(a^n\). Решение оформите в виде функции power(a, n).
Стандартной функцией или операцией возведения в степень пользоваться нельзя.
Входные данные
Вводится действительное положительное число \(a\) и целоe число \(n\).
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
2 1
Выходные данные
2
Входные данные
2 2
Выходные данные
4
Даны два натуральных числа \(n\) и \(m\). Сократите дробь \(\frac{n}{m}\), то есть выведите два других числа \(p\) и \(q\) таких, что \(\frac{n}{m}=\frac{p}{q}\) и дробь \(\frac{p}{q}\) — несократимая.
Решение оформите в виде функции ReduceFraction(n, m), получающая значения
n и m и возвращающей кортеж из двух чисел.
Входные данные
Вводятся два натуральных числа.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
12 16
Выходные данные
3 4
#3798
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число \(n>1\). Выведите его наименьший простой делитель.
Решение оформите в виде функции MinDivisor(n). Алгоритм должен
иметь сложность \(O(\sqrt{n})\).
Указание. Если у числа \(n\) нет делителя не превосходящего \(\sqrt{n}\), то число \(n\) — простое и ответом будет само число \(n\).
Входные данные
Вводится натуральное число.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
4
Выходные данные
2
Входные данные
5
Выходные данные
5
Выбрано
:
|