--->
260 задач
<---
Источники
Дана последовательность чисел, завершающаяся числом 0. Найдите сумму всех этих чисел, не используя цикл.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся числом 0 (само число 0 в последовательность не входит, а служит как признак ее окончания).
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
1 7 9 0
Выходные данные
17
Дана последовательность целых чисел, заканчивающаяся числом 0. Выведите эту последовательность в обратном порядке.
При решении этой задачи нельзя пользоваться массивами и прочими динамическими структурами данных. Рекурсия вам поможет.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся числом 0.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
1 2 3 0
Выходные данные
0 3 2 1
Возводить в степень можно гораздо быстрее, чем за \(n\) умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
\(a^n=(a^2)^{n/2}\) при четном \(n\),
\(a^n=a\cdot a^{n-1}\) при нечетном \(n\).
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет \(O(\log n)\).
Входные данные
Вводится действительное число a и целое неотрицательное число n.
Выходные данные
Выведите ответ на задачу.
Нельзя использовать стандартное возведение в степень.
Примеры
Входные данные
2 7
Выходные данные
128
Входные данные
1.00001 100000
Выходные данные
2.71827
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Для быстрого вычисления наибольшего общего делителя двух чисел используют алгоритм Евклида. Он построен на следующем соотношении: \(НОД(a, b)=НОД(b, a\bmod b)\).
Реализуйте рекурсивный алгоритм Евклида в виде функции gcd(a, b).
Входные данные
Вводится два целых числа.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
12 14
Выходные данные
2
Входные данные
256 48
Выходные данные
16
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из \(n\) дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите программу, которая решает головоломку; для данного числа дисков n
печатает последовательность перекладываний в формате
a b c, где a — номер перекладываемого диска,
b — номер стержня с которого снимается данный диск,
c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня
2 на стержень 3. В одной строке печатается одна команда.
Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.
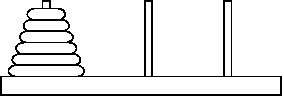
Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков? Из четырех дисков? Пусть мы научились перекладывать пирамидку из \(n\) дисков с произвольного стержня на любой другой, как переложить пирамидку из \(n+1\) диска, если можно пользоваться решением для \(n\) дисков.
Напишите функцию move (n, x, y),
которая печатает последовательнось перекладываний дисков для перемещения
пирамидки высоты n со стержня номер x
на стержень номер y.
Входные данные
Вводится натуральное число - количество дисков.
Выходные данные
Выведите ответ на задачу.
Примеры
Входные данные
2
Выходные данные
1 1 2 2 1 3 1 2 3
Выбрано
:
|