Шрам хочет остаться единственным претендентом на титул короля Саванны. Ради этого он коварно расправился с Муфасой, после чего приказал своим приспешникам-гиенам уничтожить Симбу. К счастью, Симбе улыбнулась удача, и ему предоставился шанс спастись от стаи разъяренных гиен.
Гиены преследуют Симбу на квадратном клетчатом поле, длина и ширина которого равны \(k\) клеткам. Как столбцы, так и строки этого поля пронумерованы числами от одного до \(k\). Симба находится в одной из клеток поля, находящейся в первой строке. Стая гиен находится в некоторой клетке поля, не совпадающей с той, в которой находится Симба.
Симба и стая по очереди перемещаются по полю. За один ход Симба должен перебежать в одну из клеток, соседних по вертикали, горизонтали, или диагонали с той, в которой он находится. После этого гиены могут переместиться в любую клетку, расстояние до которой по горизонтали совпадает с расстоянием по вертикали. Проще говоря, гиены могут переместиться в любую клетку, находящуюся на одной диагонали с той, в которой они располагаются в данный момент.
Если после чьего-либо хода гиены оказываются в одной клетке с Симбой, будущий король погибает в неравной схватке. Если же после очередного ходя львенка он оказывается в любой из клеток \(k\)-й строки, в которой нет гиен, он благополучно пересекает поле и скрывается в джунглях. Помогите Симбе сбежать от своих преследователей.
В первой строке программа жюри передает вашей программе одно целое число \(k\) (\(3 \le k \le 100\)) — размер поля, которое необходимо пересечь Симбе. В следующей строке программа жюри передает одно целое число \(b\) (\(1 \le b \le k\)) — номер столбца, в котором находится клетка с Симбой. В следующей строке программа жюри передает два целых числа \(x\) и \(y\) (\(1 \le x, y \le k\)) — номера строки и столбца клетки, в которой находится стая гиен. Гарантируется, что эта клетка не является клеткой с Симбой. После этого несколько раз повторяются следующие действия.
Ваша программа передает два целых положительных числа, не превышающих \(k\) — номера строки и столбца клетки, в которую необходимо переместиться Симбе. После этого программа жюри передает вашей программе два целых положительных числа, не превышающих \(k\) — номера строки и столбца клетки, в которую перемещается стая гиен.
В случае, если после очередного хода Симбы он оказался в клетке строки с номером \(k\), в которой нет гиен, завершите программу — это будет означать успешный побег Симбы. За все время работы программы Симба должен сделать не более 1000 ходов.
4 1 4 4 2 2 3 1
2 1 3 2 4 2
Для корректной работы программы после каждой операции вывода данных вам необходимо делать следующие операции:
- В языке Pascal: flush(output)
- В C/C++: fflush(stdout)
- В Java: System.out.flush()
- В Python: sys.stdout.flush()
Кроме этого, не забывайте после каждой выведенной строки ставить перевод строки.
Джейкоб думает очень громко.
Эдвард
Все вампиры обладают уникальной способностью читать мысли, и Эдвард очень часто пользовался ей для защиты своей жены Беллы Свон. Поэтому, когда на нее напали несколько вампиров клана Вольтури, он тут же решил прочитать их мысли, дабы узнать мощь каждого напавшего вампира.
Но каждый вампир этого клана обладает ментальным щитом, поэтому узнать мощь отдельного вампира невозможно. Эдвард может лишь узнать сумму всех чисел, выражающих их мощь, но при этом он может брать каждое число с нужным ему знаком (плюс или минус).
Эдварду срочно необходима ваша помощь, иначе Беллу съедят вампиры из клана Вольтури.
Программа жюри выводит число \(n\) в отдельной строке (\(1 \le n \le 100\)). После этого не более чем \(n\) раз повторяются следующие действия.
Ваша программа выводит в отдельной строке строку, состоящую из символов \(a_i\) (\(a_i = \) + или \(a_i = \) -), разделенных пробелами, где \(i\)-й символ означает, с каким знаком мы просуммируем мощь \(i\)-го вампира \(p_i\) (\(-100 \le p_i \le 100\)).
Когда вы найдете мощь каждого вампира, вашей программе необходимо вывести в строчку их все по порядку:
где \(a_i\) — мощь i-го вампира.
2 3 -1
+ + + - answer: 1 2
Для корректной работы программы после каждой операции вывода данных вам необходимо делать следующие операции:
- В языке Pascal: flush(output)
- В C/C++: fflush(stdout)
- В Java: System.out.flush()
- В Python: sys.stdout.flush()
Кроме этого, не забывайте после каждой выведенной строки ставить перевод строки.
Школьники готовятся к участию в соревновании по программированию квадрокоптеров. Квадрокоптер, который используется в соревновании, может выполнять две команды: подняться вверх на 1 метр и опуститься вниз на 1 метр. Команда подъёма обозначается символом «(», а команда спуска — символом «)».
Программа для квадрокоптера представляет собой последовательность команд. Программа считается корректной, если, начав её исполнение на уровне земли и выполнив последовательно все команды, квадрокоптер снова оказывается на уровне земли. При этом в процессе выполнения программы квадрокоптер не должен пытаться опуститься ниже уровня земли.
Например, следующие программы являются корректными: «()(())», «((()))». Программа«(((» не является корректной, поскольку квадрокоптер завершает ее выполнение на высоте 3 метра над уровнем земли, программа «())(» также не является корректной, поскольку при выполнении третьей команды квадрокоптер пытается опуститься ниже уровня земли.
Участник соревнования написал корректную программу для квадрокоптера, состоящую из n команд, пронумерованных от 1 до n. Он загрузил её в память квадрокоптера для демонстрации во время соревнования. К сожалению, после загрузки программы в память квадрокоптера участник случайно удалил её на своём компьютере, а квадрокоптер не позволяет выгрузить программу из своей памяти.
К счастью, квадрокоптер поддерживает специальный режим отладки программы. В этом режиме квадрокоптер с загруженной в него программой может отвечать на специальные запросы. Каждый запрос представляет собой два целых числа: l и r, 1 ≤ l ≤ r ≤ n. В ответ на запрос квадрокоптер сообщает, является ли фрагмент загруженной в него программы, состоящий из команд с l-й по r-ю включительно, корректной программой для квадрокоптера, либо нет. Участник хочет с помощью режима отладки восстановить загруженную в квадрокоптер программу.
Требуется написать программу-решение, которая взаимодействует с программой жюри, моделирующей режим отладки квадрокоптера, и в итоге восстанавливает загруженную в квадрокоптер программу.
Это интерактивная задача.
Сначала на вход подаётся целое число n — количество команд в программе квадрокоптера (2 ≤ n ≤ 50 000).
Для каждого теста жюри зафиксировано число k — максимальное количество запросов. Гарантируется, что k запросов достаточно, чтобы решить задачу. Это число не сообщается программе-решению. Ограничения k в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов к программе жюри, то на этом тесте она получает в качестве результата тестирования «Неверный ответ».
Чтобы сделать запрос, программа-решение должна вывести строку вида «? l r», где l и r — целые положительные числа, задающие фрагмент программы квадрокоптера (1 ≤ l ≤ r ≤ n).
В ответ на запрос программы-решения программа жюри подаёт ей на вход либо строку «Yes», либо строку «No», в зависимости от того, является ли запрошенный фрагмент программы квадрокоптера корректной программой.
Если программа-решение определила ответ на задачу, то она должна вывести строку «! c1c2... cn», где символ ci задаёт i-ю команду в программе квадрокоптера и равен либо «(», либо «)».
После этого программа-решение должна завершиться.
Гарантируется, что в каждом тесте программа в памяти квадрокоптера является фиксированной корректной программой, которая не меняется в зависимости от запросов, произведённых программой-решением.

Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.
В первом примере n = 4. Единственная возможная корректная программа из двух команд это «()», поэтому из результатов третьего и четвёртого запросов можно сделать вывод, что программа в памяти квадрокоптера — «()()». Поэтому, в частности, ответ на второй запрос действительно «No», так как фрагмент программы «()(» не является корректной программой: если квадрокоптер исполнит именно эти три команды, он останется на уровне одного метра над землёй.
В втором примере n = 6, и произведённых запросов достаточно, чтобы однозначно определить, что программа в памяти квадрокоптера — «((()))».
В тестах из условия k = 150, то есть, разрешается произвести не более 150 запросов.

В заповеднике живут q тигров. Чтобы следить за положением тигров на территории заповедника, используются ошейники с радиомаяком. Ошейник у каждого тигра имеет радиомаяк с уникальным сигналом. Система обнаружения настраивается на приём сигнала радиомаяка от i-го тигра последовательно для i от 1 до q.
Для приёма сигнала на территории заповедника установлено n приёмников в точках с координатами (x1, y1), ..., (xn, yn). Система обнаружения позволяет сотруднику заповедника за один запрос выбрать любые m (3 ≤ m ≤ n) приёмников. Выбранные приёмники должны являться вершинами выпуклого многоугольника. Система определяет, находится ли радиомаяк i-го тигра внутри этого многоугольника.
Сотрудник заповедника должен локализовать положение каждого тигра. Положение i-го тигра считается локализованным, если удалось определить такое множество приёмников, являющихся вершинами выпуклого многоугольника, что внутри этого многоугольника находится тигр, но нет других приёмников.
Для того, чтобы локализовать положение каждого из тигров, сотруднику разрешается сделать не более k запросов.
После того как положение i-го тигра локализовано, система автоматически переходит к приёму сигналов от следующего тигра, пока положение всех q тигров не будет локализовано.
Гарантируется, что никакие три приёмника не лежат на одной прямой, и ни один тигр не находится на прямой, проходящей через два приёмника. Гарантируется, что существует хотя бы один выпуклый многоугольник с вершинами в приёмниках, внутри которого находится тигр.
Требуется написать программу, которая взаимодействует с программой жюри и локализует положение каждого тигра.
Это интерактивная задача.
Сначала на вход подаётся информация об установленных в заповеднике приёмниках и количестве тигров.
Первая строка входных данных содержит целое число n — количество приёмников (3 ≤ n ≤ 5 000). Последующие n строк описывают координаты приёмников, j-я из этих строк содержит два целых числа xj и yj — координаты j-го приёмника ( - 109 ≤ xj, yj ≤ 109). Следующая строка содержит число целое число q — количество тигров (1 ≤ q ≤ 2000).
Для локализации положения тигров необходимо выполнять запросы к системе обнаружения, роль которой выполняет программа жюри.
Для каждого теста зафиксировано число k — максимальное количество запросов к системе обнаружения для локализации положения одного тигра. Гарантируется, что k запросов достаточно, чтобы решить задачу для соответствующих данных. Это число не сообщается программе-решению, но ограничения на него в различных подзадачах приведены в таблице системы оценивания. Если программа-решение делает более k запросов для определения местоположения одного из тигров, на этом тесте она получает в качестве результата тестирования «Неверный ответ».
Запрос к системе обнаружения начинается с символа «?», за которым следует целое число m — количество выбранных в запросе приёмников (3 ≤ m ≤ n), и m различных целых чисел pi — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ pi ≤ n).
В ответ программа получает строку «Yes», если тигр находится внутри многоугольника, образованного приёмниками с номерами p1, ..., pm, и строку «No» в противном случае.
После того, как положение тигра локализовано, программа-решение должна вывести строку, начинающуюся с символа «!», за которым следует целое число m — количество выбранных приёмников (3 ≤ m ≤ n), и m различных целых чисел pi — номера приёмников, перечисленные в порядке обхода многоугольника по или против часовой стрелки (1 ≤ pi ≤ n). Эта строка означает, что внутри выпуклого многоугольника, образованного приёмниками с номерами p1, ..., pm, находится тигр и нет других приёмников.
Ответное сообщение от программы жюри отсутствует, и программа-решение должна немедленно приступать к поиску следующего тигра. Локализовав положение тигра с номером q, программа-решение должна завершить работу.
Тигры не перемещаются во время работы системы обнаружения. Координаты тигров в каждом тесте фиксированы и не меняются в процессе тестирования.
Если существует несколько правильных многоугольников, локализующих положение тигра, можно вывести любой из них.
На рисунке продемонстрирована процедура локализации положения каждого из тигров из приведенного ниже примера.


Приведённые примеры иллюстрируют взаимодействие программы-решения с программой жюри «по шагам», для чего в них добавлены дополнительные пустые строки. При реальном тестировании лишние пустые строки вводиться не будут, выводить пустые строки также не требуется.
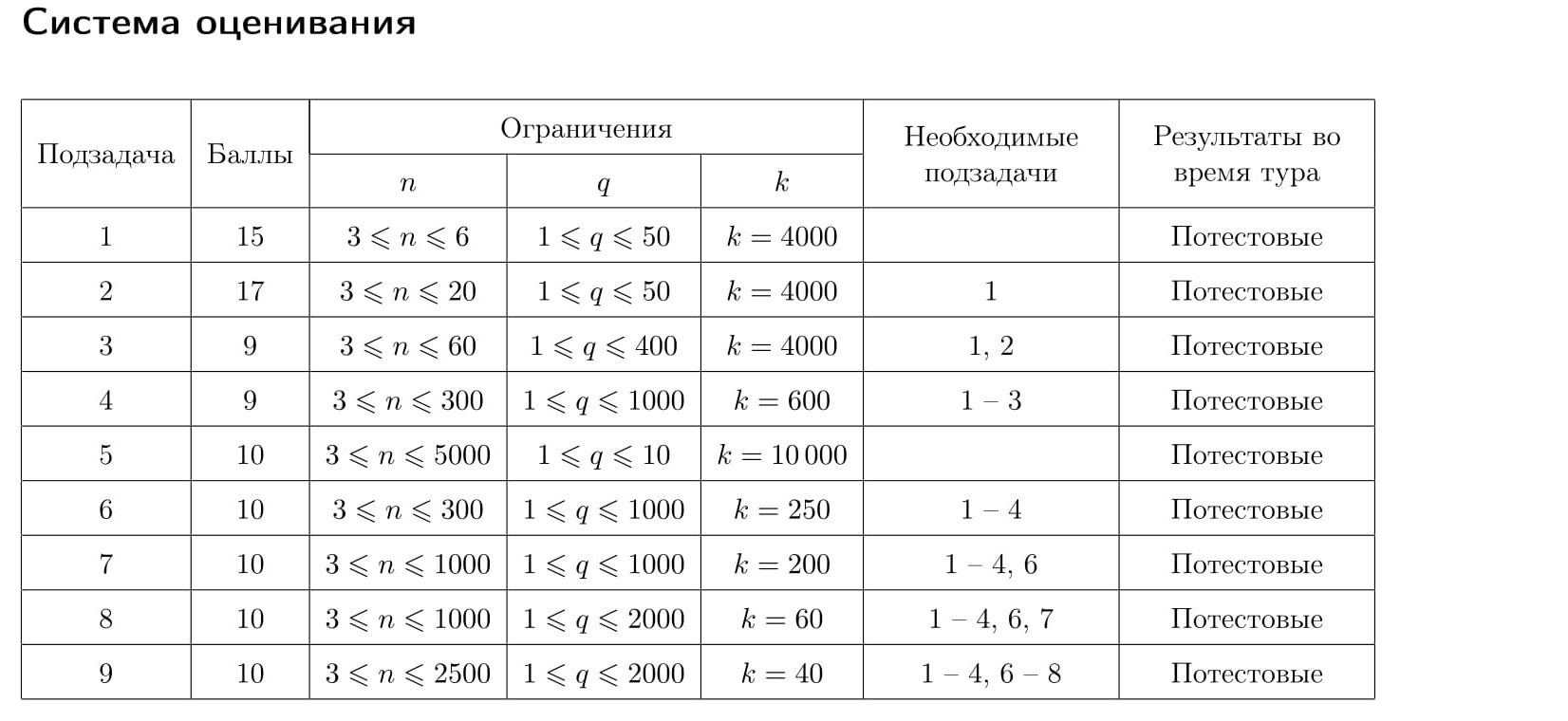
Это интерактивная задача.
В былые времена гномы пытались развить у себя экстрасенсорные способности:
- В абсолютно тёмную пещеру заводили n гномов.
- На каждого гнома надевали шляпу — белую или чёрную. Гномы в пещере не видели цветов своих шляп и шляп других гномов.
- Гномы по очереди выходили из пещеры на поляну и садились на произвольное места. При этом, выходя из пещеры, каждый гном видел цвета шляп всех гномов, вышедших ранее. Тем не менее, он не видит цвет собственной шляпы и никто из других гномов ему этот цвет не сообщает.
- Задача состояла в том, чтобы все гномы разошлись в две стороны — в одну те, кто носят белые шляпы и в другую — чёрные.
За многие века гномы научились безошибочно выбирать для себя место на поляне. Получится ли подобное у вас?
Вас просят по очереди назвать n различных точек на плоскости с целочисленными координатами. После указания очередной точки вам будет сообщён её цвет — чёрный или белый. Ваша задача — добиться того, чтобы названные точки можно было разбить прямой так, чтобы точки одного цвета лежали по одну сторону от прямой, точки разного цвета — по разные стороны и никакие точки не лежали на прямой. Также вы должны предъявить такую прямую.
В данной задаче интерактор является адаптивным — цвета точек в тесте заранее не зафиксированы и программа жюри может выбирать их произвольным образом, в том числе учитывая вывод вашей программы.
В первой строке стандартного потока ввода дано целое число n ( 1 ≤ n ≤ 30 ) — количество точек, которое должна назвать ваша программа.
Затем n раз ваша программа должна вывести по два целых числа x и y ( 0 ≤ x ≤ 10 9 , 0 ≤ y ≤ 10 9 ) — координаты очередной точки. Все выведенные вами точки должны быть различными.
В ответ на каждую пару координат ваша программа получит на вход строку « black », если точка имеет чёрный цвет, или « white », если точка имеет белый цвет.
После того, как все n точек будут обработаны, вы должны вывести четыре целых числа x 1 , y 1 , x 2 и y 2 ( 0 ≤ x 1 , y 1 ≤ 10 9 , 0 ≤ x 2 , y 2 ≤ 10 9 ) — координаты точек ( x 1 , y 1 ) и ( x 2 , y 2 ) , через которые проходит прямая, разделяющая n точек на белые и чёрные. Точки ( x 1 , y 1 ) и ( x 2 , y 2 ) не должны совпадать.
В условии в примере взаимодействия вводимые и выводимые данные расположены для удобства восприятия в хронологическом порядке, при реальном взаимодействии никакие «лишние» переводы строк возникать не должны.
Иллюстрация к первому примеру.
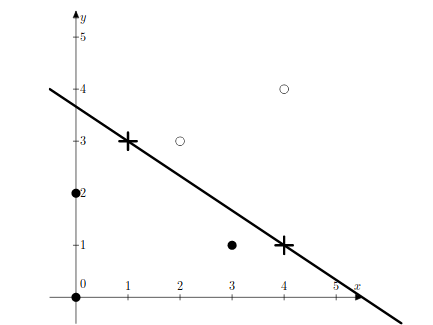
5 black black white white black
0 0 3 1 2 3 4 4 0 2 1 3 4 1