Страница: 1 Отображать по:

#114086

Шаровая машина

Источники: [ Личные олимпиады, Baltic Olympiad in Informatics, Baltic Olympiad in Informatics 2013, Шаровая машина ]

У нас есть «шаровая машина», которую можно представить как корневое дерево. Узлы дерева пронумерованы от $1$ до $N$. каждый узел либо пуст, либо содержит один шар. Изначально все узлы пусты. В то время работы, машина может выполнить 2 разные операций:

Добавить $K$ шаров машину: шарики добавляются по одному в узел корня. Если у шара есть пустой узел прямо под ним, он будет скатываться вниз. Если имеется несколько пустых дочерних узлов, шар выберет узел с наименьшим числом в его поддереве. Если же мяч скатывается вниз на несколько уровней, он делает выбор на каждом уровне. Например: если мы добавим два шарики к машине на картинке ниже, они пойдут к узлам $1$ и $3$: первый шарик из узла $4$ к узлу $3$, потому что узел $3$ пуст и содержит узел $1$ в своем поддереве (которое состоит узлов $3$ и $1$); он далее катится от узла $3$ к узлу $1$. Второй шарик катится от узла 4 к узлу $3$ останавливается там. $\text{[math]}$
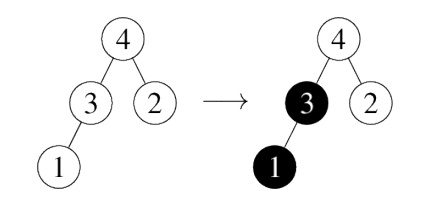
Удалить шар из указанного узла: этот узел становится пустым и шары сверху (если таковые есть) скатываются вниз. Всякий раз, когда родитель пустого узла содержит шар, этот шар будет скатываться вниз. Если удалить шарики из узлов $5$, $7$ и $8$ (именно в этом порядке) из машины на рисунке ниже, узлы $1$, $2$ и $3$ станут пустыми. $\text{[math]}$

Входные данные

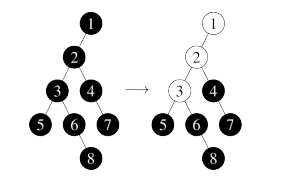
Первая строка содержит два целых числа $N$ и $Q$ ($1 \leq N, Q \leq 100\,000$) – количество узлов дерева и количество операций соответственно. Следующие $N$ строк описывают шаровую машину. Каждая из этих строк содержит одно целое число, номер узла: $i$-я из этих строк содержит номер родительского узла вершины $i$ или $0$, если узел $i$ является корнем дерева. Каждая из следующих $Q$ строк содержит по два целых числа и описывает операцию, которую необходимо выполнить. Операция типа $1$ обозначается $1 k$ , где $k$-количество шариков, добавляемых в машину. Операция типа $2$ обозначается $2 x$ , где $x$-номер узла, из которого должен быть удален шар. Гарантируется, что все выполняемые операции верны: операции не требуют добавления большего количества шаров, чем есть пустые узлы в шаровой машине, или удаления шара из пустого узла.

Выходные данные

Для каждой операции типа $1$ выведите номер узла, в котором оказался последний вставленный шар. Для каждой операции типа $2$ выведите количество шариков, которые скатились вниз после удаления шарика из указанного узла.

Система оценки

Подзадача 1 (25 баллов): каждый узел имеет 0 или 2 дочерних элемента. Кроме того, все узлы с 0 дети находятся на одинаковом расстоянии от корня.

Подзадача 2 (25 баллов): операции будут запрошены таким образом, что никакие шары никогда не скатываются после операции типа 2.

Подзадача 3 (25 баллов): есть ровно одна операция типа 1, и это самая первая операция.

Подзадача 4 (25 баллов): нет доп. ограничений.

Примеры

Входные данные

Выходные данные

Страница: 1 Отображать по:

Выбрано

Отменить

Добавить в контест