Магазины в рекламных целях часто устраивают распродажи. Так, например,одна из крупных сетей магазинов канцелярских товаров объявила два рекламных предложения: "купи \(N\) одинаковых товаров и получи еще один товар бесплатно"и "купи \(K\) товаров по цене \(K-1\) товара".
Для проведения олимпиады организаторам требуется распечатать условия для участников, на что уходит очень много бумаги. Каждая пачка стоит \(B\) рублей. Какое максимальное количество пачек бумаги можно приобрести на \(A\) рублей, правильно используя рекламные предложения?
Во входном файле записаны целые числа \(N\), \(K\), \(A\) и \(B\) (\(1\leq N\leq 100\), \(2\leq K\leq 100\), \(1\leq A \leq 10^9\), \(1\leq B \leq 10^9\)), разделенные пробелами.
Выведите одно целое число - максимальное количество пачек бумаги, которое смогут купить организаторы олимпиады.
В первом примере, дважды используя второе рекламное предложение, можно купить 8 пачек бумаги, заплатив за 6.
Во втором примере рекламными предложениями воспользоваться нельзя.
В третьем примере можно по одному разу воспользоваться каждым из двух рекламных предложений и на оставшийся рубль купить еще одну пачку бумаги.
4 4 13 2
8
3 4 8 3
2
3 4 7 1
9
Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.
Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.
Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.
Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.
Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит \(10^5\) символов.
Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.
Выведите одно целое число - минимальное количество переправ.
Рисунок к приведенному выше примеру.
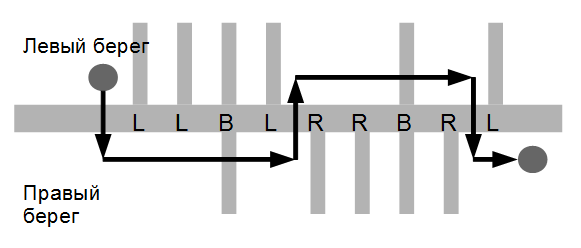
LLBLRRBRL
5