На протяжении многих лет Вася работает программистом в одной очень большой и очень известной компании. Эта компания обеспечивает своих сотрудников всем необходимым для приятной
и плодотворной работы: бесплатными обедами, транспортом от дома до места работы и многим,
многим другим. И вот в один прекрасный солнечный день Вася понял, что ему очень наскучил вид
из окна его офиса, и ему нужно, чтобы за окном было что-то новое и прекрасное. А что может быть
лучше чудесного горного пейзажа? Придя к этой мысли, Вася попросил своего менеджера подобрать
себе новый офис с красивым видом на горы.
В той местности, где располагается офис Васи, каждая гора принадлежит некоторой горной
цепи. Так как Васе хочется, чтобы вид из окна его офиса был идеальным, то он попросил подобрать
себе такой офис, чтобы никакие две горные цепи, видимые из окна, не пересекались. Менеджер
Васи нашел прекрасный новый офис, из которого видно N горных цепей, но он никак не может
определить, понравится ли Васе вид из окна этого офиса. Помогите ему!
Более формально, вид из окна офиса представляет собой набор горных цепей, пронумерованных
от \(1\) до \(N\), где горная цепь с номером i представляет собой ломаную на плоскости из \(l_i\) звеньев с
вершинами в точках (\(x_i\),\(j\) , \(y_i\),\(j\) ), причем для любых \(i\), \(j\) выполнено \(x_{i,j} < x_{i,j+1}\).
Кроме этого, окно в офисе имеет фиксированную ширину, поэтому все горные цепи начинаются
и заканчиваются на одной вертикали, то есть существуют такие числа \(A\) и \(B\), что для любого номера
\(i\) горной цепи выполнено \(x_{i,0} = A, x_{i,l_i} = B\).
Отметим, что из определения горной цепи следует, что для любого значения абсциссы \(A \le x \le B\)
на ломаной с номером \(i\) существует единственная точка (\(x\), \(y_i\)(\(x\))) с этим значением абсциссы, принадлежащая этой ломаной. Будем говорить, что горная цепь \(i\) находится строго выше горной цепи
\(j\) в точке \(x\), если выполнено строгое неравенство \(y_i(x) > y_j (x)\).
Естественно считать, что цепь под номером \(i\) пересекается с цепью под номером \(j\), если существуют такие два значения абсциссы \(x_1\), \(x_2\), что цепь \(i\) находится строго выше цепи \(j\) в точке
\(x_1\), но при этом цепь \(j\) находится строго выше цепи \(i\) в точке \(x_2\), то есть выполнены неравенства
\(y_i\)(\(x_1\)) > \(y_j\) (\(x_1\)) и \(y_j\) (\(x_2\)) > \(y_i\)(\(x_2\)). Обратите внимание на поясняющие рисунки, расположенные в
примечании к задаче.
Вам необходимо определить, подойдет ли подобранный офис Васе, и, если нет, то найти любую
пару пересекающихся горных цепей.
Замечание
Напоминаем, что абсциссой точки называется её \(x\)-координата, а ординатой — её \(y\)-координата.
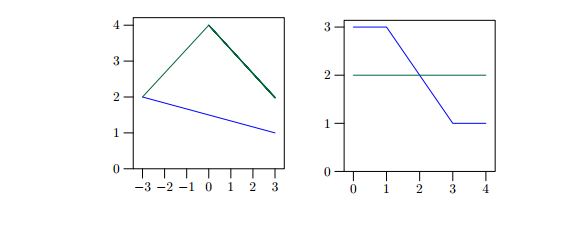
В первом примере хотя ломаные и касаются друг друга в точке (−3, 2), но, согласно данному
выше определению, они не пересекаются.
Во втором примере в точке \(x_1\) = 1 одна ломаная выше другой, а в точке \(x_2\) = 3 — наоборот, то
есть горные цепи пересекаются.
