Дано натуральное число N. Требуется представить его в виде суммы двух натуральных чисел A и B таких, что НОД (наибольший общий делитель) чисел A и B — максимален.
Ограничение по времени выполнения программы - 1 секунда, ограничение по используемой памяти - 64 мегабайта.
Во входном файле записано натуральное число N (2≤N≤109)
В выходной файл выведите два искомых числа A и B. Если решений несколько, выведите любое из них.
15
5 10
16
8 8
Петя решил зашифровать свой дневник, чтобы никто без его ведома не смог его прочитать. Для этого он воспользовался следующим шифром.
Он изготовил трафарет NxN клеток (N — четное), в котором вырезал клеток так, что при наложении трафарета на лист бумаги четырьмя возможными способами (трафарет можно поворачивать, но нельзя переворачивать) каждая клетка листа видна ровно один раз.
Пример такого трафарета показан на рисунке ниже:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С помощью этого трафарета шифруется текст из N2 символов следующим образом. Сначала в прорези трафарета вписываются первые букв шифруемого текста (буквы вписываются в вырезанные клетки по строкам сверху вниз, в каждой строке — слева направо). Например, если Петя шифрует слово ОЛИМПИАДА, то оно будет вписано в клетки следующим образом:
| О |
|
|
| Л |
|
|
| И |
| М |
|
|
|
|
|
|
| П |
|
|
|
| И |
|
| А |
| Д |
|
|
|
|
|
|
|
|
| А |
|
|
Далее трафарет поворачивается на 90 градусов по часовой стрелке, и в вырезанные клетки в том же порядке вписываются следующие букв шифруемого текста. И так далее. Если шифруемый текст состоит меньше, чем из N2 символов, то (когда текст кончается) оставшиеся клетки остаются пустыми.
Например, если Петя шифрует текст ОЛИМПИАДА ПО ИНФОРМАТИКЕ 2006 ГОДА при помощи приведенного трафарета, то процесс шифрования будет устроен так. Как зашифровать слово ОЛИМПИАДА, мы уже показали. Для удобства здесь и далее пробел будем обозначать знаком подчеркивания. При втором прикладывании трафарета Пете удастся зашифровать _ПО_ИНФОР:
| О | _ |
|
| Л | П |
|
| И |
| М | О |
|
|
|
| _ |
| П |
|
| И |
| И |
| Н | А |
| Д |
|
| Ф |
| О |
|
|
| Р | А |
|
|
При третьем прикладывании трафарета Петя зашифрует МАТИКЕ_20:
| О | _ | М |
| Л | П |
|
| И |
| М | О | А |
| Т |
| _ | И | П |
|
| И | К | И |
| Н | А |
| Д |
| Е | Ф | _ | О |
|
| 2 | Р | А |
| 0 |
При четвертом прикладывании трафарета Петя зашифрует 06_ГОДА. Остальные клетки окажутся пустыми (будем считать, что в них записан пробел, который мы обозначаем подчеркиванием):
| О | _ | М | 0 | Л | П |
| 6 | И | _ | М | О | А |
| Т | Г | _ | И | П | О |
| И | К | И | Д | Н | А |
| Д | А | Е | Ф | _ | О |
| _ | 2 | Р | А | _ | 0 |
После этого получившийся текст Петя выписывает в строчку:
О М0ЛП6И МОАТГ ИПОИКИДНАДАЕФ О 2РА 0
Для повышения надежности Петя решил зашифрованный текст зашифровать тем же методом с помощью того же трафарета еще раз, затем получившийся текст — еще раз и т.д. После нескольких повторов Петя с удивлением заметил, что зашифрованный текст совпал с исходным.
Напишите программу, которая для данного трафарета определит, после какого наименьшего количества процедур шифрования Петя получит исходный текст независимо от содержания текста?
Сначала во входном файле записано число N — размер трафарета (2≤N≤150). Затем идет N2 чисел (каждое из которых 0 или 1), описывающих трафарет. 1 обозначает вырезанную клетку, 0 — не вырезанную. Гарантируется, что данная последовательность описывает корректный трафарет для данного способа шифрования.
В выходной файл выведите одно число — через какое минимальное количество повторов операции шифрования Петя получит исходный текст независимо от его содержания.
2 1 0 0 0
2
6 1 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 1 0 0
120
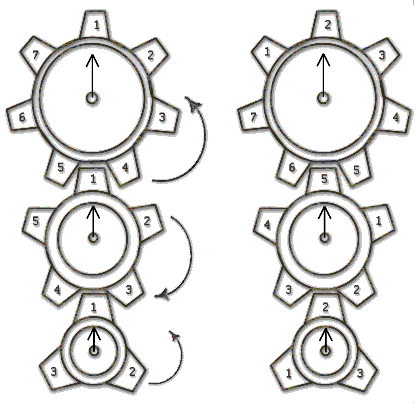 На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a1,a2,a3), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.
На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке n зубцов, на второй — m, на третьей — k. На каждом зубце первой, второй и третьей шестеренок по часовой стрелке написаны в порядке возрастания числа от 1 до n, от 1 до m и от 1 до k соответственно. Стрелки зафиксировали таким образом, что когда стрелка первой оси указывает на число, стрелки двух других осей также указывают на числа. Витя записывает три числа (a1,a2,a3), на которые указывают стрелки. После этого он поворачивает первую шестеренку на угол 360°/n против часовой стрелки, чтобы напротив стрелки на первой оси оказался следующий (по часовой стрелке) зубец. При этом вторая шестеренка поворачивается на угол 360°/m по часовой стрелке (размеры зубцов у шестеренок одинаковые, поэтому размеры самих шестеренок разные, чтобы на границе шестеренок равномерно уложилось разное число одинаковых по размеру зубцов), а третья шестеренка поворачивается на угол 360°/k против часовой стрелки. Витя опять записывает три числа, на которые указывают стрелки.
Поступая и далее таким образом, Витя заметил, что после некоторого количества таких действий стрелки показывают на три первоначальных числа.
Теперь его очень интересует, как по двум данным тройкам чисел определить, принадлежат ли они к одной последовательности, то есть можно ли некоторым количеством поворотов перейти от первой тройки ко второй. Он попросил вас написать программу, которая отвечает на этот вопрос.
В первой строке содержатся четыре числа T, n, m, k (1 ≤ T ≤ 10, 1 ≤ n, m, k ≤ 1018) — количество пар троек, которые хочет проверить Витя и количества зубцов соответственно на первой, второй и третьей шестеренках.
В следующих T строках записаны шесть натуральных чисел a1, a2, a3, b1, b2, b3 (1 ≤ a1, b1 ≤ n, 1 ≤ a2, b2 ≤ m, 1 ≤ a3, b3 ≤ k).
Для каждой пары троек в выходной файл выведите YES, если обе тройки принадлежат одной последовательности, и NO иначе. Каждое слово должно быть в отдельной строке, в порядке, соответствующем входному файлу.
Комментарии к примерам тестов
1. В первой и второй парах вторая тройка получается из первой за один поворот первой шестеренки против часовой стрелки.
В третьем случае из второй конфигурации просто получить первую опять же одним поворотом первой шестеренки против часовой стрелки.
Очевидно, что тогда из первой можно каким-то образом получить вторую.
2. В первой паре тройки нельзя перевести друг в друга.
Во второй тройки переходят друг в друга при одном повороте.
3. (1, 1, 1) — (семь поворотов первой против часовой стрелки шестеренки) — (1, 4, 2) — (еще семь таких же поворотов) — (1, 2, 3) — (один поворот) — (2, 1, 1)
Частичные ограничения
Первая группа состоит из тестов, в которых произведение nmk ≤ 106.
Вторая группа состоит из тестов, в которых n, m, k ≤ 109.
Примечание
Не гарантируется, что описанную в условии задачи систему шестеренок и стрелок можно реально построить.
3 11 13 15 5 5 5 6 4 6 11 13 15 1 12 1 2 13 2 1 1 1
YES YES YES
2 2 2 2 1 1 1 1 1 2 1 1 1 2 2 2
NO YES
1 7 5 3 1 1 1 2 1 1
YES