Страница: 1 2 >> Отображать по:
#45
Контейнеры
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

На складе хранятся контейнеры с товарами N различных видов. Все контейнеры составлены в N стопок. В каждой стопке могут находиться контейнеры с товарами любых видов (стопка может быть изначально пустой).Автопогрузчик может взять верхний контейнер из любой стопки и поставить его сверху в любую стопку. Необходимо расставить все контейнеры с товаром первого вида в первую стопку, второго вида — во вторую стопку и т.д.

Программа должна вывести последовательность действий автопогрузчика или сообщение о том, что задача решения не имеет.

Входные данные

В первой строке задается одно натуральное число N, не превосходящее 500. В следующих N строках описаны стопки контейнеров: сначала записано число ki — количество контейнеров в стопке, а затем ki чисел — виды товара в контейнерах в данной стопке, снизу вверх. В каждой стопке вначале не более 500 контейнеров (в процессе переноса контейнеров это ограничение может быть нарушено).

Выходные данные

Выведите описание действий автопогрузчика: для каждого действия укажите два числа — из какой стопки брать контейнер и в какую стопку класть. (Обратите внимание, что минимизировать количество операций автопогрузчика не требуется.) Если задача не имеет решения, выдайте одно число 0. Если контейнеры изначально правильно размещены по стопкам, выводить ничего не надо.

Оценка задачи

1 балл будут получать программы, верно работающие при следующих ограничениях: количество стопок не больше 10, в каждой стопке не более 10 контейнеров.

Комментарий к примеру:

Изначально в первой стопке лежат четыре контейнера — снизу контейнер с товаром первого вида, над ним — с товаром второго вида, над ним — третьего, и сверху — еще один контейнер с товаром второго вида.

Одна из правильных последовательностей действий (вместо ответа в примере задачи):

1 2
1 3
1 2

Примеры
Входные данные
3
4 1 2 3 2
0
0
Выходные данные
1
#855
Сортировка вагонов
  
Необходимо упорядочить числа с помощью стека.

К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

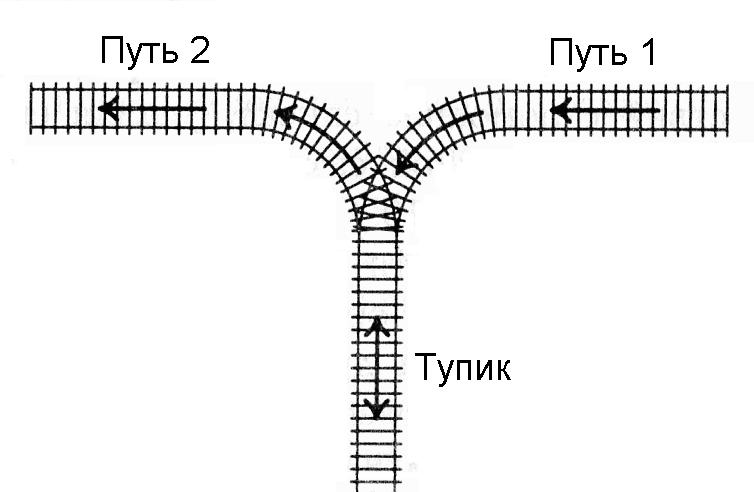
Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика).

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤2000). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите действия, которые нужно проделать с поездом. Каждое действие описывается двумя числами: типом и количеством вагонов:

  • если нужно завезти с пути 1 в тупик K вагонов, должно быть выведено сначала число 1, а затем — число K (K≥1),
  • если нужно вывезти из тупика на путь 2 K вагонов, должно быть выведено сначала число 2, а затем — число K (K≥1).

Если возможно несколько последовательностей действий, приводящих к нужному результату, выведите любую из них.

Если выстроить вагоны по порядку невозможно, выведите одно число 0.

Примеры

Входные данные

Выходные данные

3

3 2 1

1 3

2 3

4

4 1 3 2

1 2

2 1

1 2

2 3

3

2 3 1

0
#869
Сортировка вагонов
  
Темы: [Стек]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Требуется определить, возможно ли сортировка последовательности чисел с помощью стека.

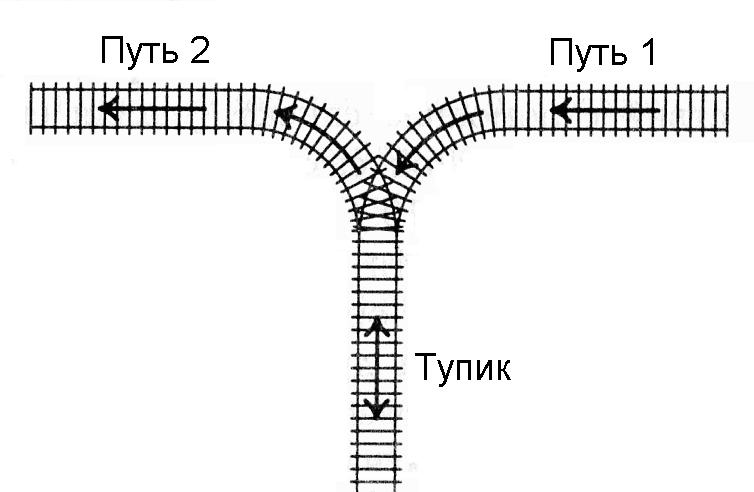
К тупику со стороны пути 1 (см. рисунок) подъехал поезд. Разрешается отцепить от поезда один или сразу несколько первых вагонов и завезти их в тупик (при желании, можно даже завезти в тупик сразу весь поезд). После этого часть из этих вагонов вывезти в сторону пути 2. После этого можно завезти в тупик еще несколько вагонов и снова часть оказавшихся вагонов вывезти в сторону пути 2. И так далее (так, что каждый вагон может лишь один раз заехать с пути 1 в тупик, а затем один раз выехать из тупика на путь 2). Заезжать в тупик с пути 2 или выезжать из тупика на путь 1 запрещается. Нельзя с пути 1 попасть на путь 2, не заезжая в тупик.

Известно, в каком порядке изначально идут вагоны поезда. Требуется с помощью указанных операций сделать так, чтобы вагоны поезда шли по порядку (сначала первый, потом второй и т.д., считая от головы поезда, едущего по пути 2 в сторону от тупика). Напишите программу, определяющую, можно ли это сделать.

Входные данные

Вводится число N — количество вагонов в поезде (1≤N≤100). Дальше идут номера вагонов в порядке от головы поезда, едущего по пути 1 в сторону тупика. Вагоны пронумерованы натуральными числами от 1 до N, каждое из которых встречается ровно один раз.

Выходные данные

Если сделать так, чтобы вагоны шли в порядке от 1 до N, считая от головы поезда, когда поезд поедет по пути 2 из тупика, можно, выведите сообщение YES, если это сделать нельзя, выведите NO.

Примеры

Входные данные Выходные данные

Комментарии

3

3 2 1

YES

Надо весь поезд завезти в тупик, а затем целиком вывезти его на 2-й путь.

4

4 1 3 2

YES

Сначала надо в тупик завезти два вагона, один из которых оставит в тупике, а второй — вывезти на 2-й путь, после чего завезти в тупик еще два вагона и вывезти 3 вагона, стоящие в тупике, на 2-й путь

3

2 3 1

NO

 
#1380
Умный чертежник
  
Линия задается набором вертикальных и горизонтальных отрезков единичной длины. Требуется изменить порядок отрезков так, чтобы линия не имела самопересечений (замена на самокасания).

Фирма "Макрохард" изобрела новое устройство с целью облегчить труд людей, кому по долгу службы приходится чертить много чертежей, а также школьников, изучающих черчение. Это устройство представляет собой крошечного робота, который умеет ползать по клетчатому листу бумаги. При этом в начале он обязательно должен быть расположен на пересечении линий сетки.

Этот робот умеет выполнять программу, которая может состоять из команд E,W,N,S — переместиться по листу в соседнюю вершину сетки вправо, влево, вперед, назад соответственно. Перемещаясь в соседний узел сетки, робот оставляет за собой ровную линию. При этом по правилам техники безопасности ему категорически запрещается проводить дважды одну и ту же линию, так как при попытке провести линию второй раз, он очень сильно пачкается в своих же собственных чернилах (они очень долго сохнут), и выходит из строя.

При этом, правда, через одну и ту же вершину сетки робот может проходить дважды. Возможно два случая (более толстой линией показано, как мы проезжаем через вершину в первый раз, более тонкой - во второй).

В первом случае мы оба раза проезжаем через вершину "прямо" (будем называть это самопересечением маршрута), а во втором случае — оба раза "поворачиваем" (это будем называть самокасанием).

Разработчики также установили, что в случае самопересечения маршрута робот пачкается в своих чернилах сильнее, чем в случае самокасания, и, если самопересечения встречаются часто, быстро выходит из строя. Поэтому они решили написать для него внутренний оптимизатор программы.

Вам дается программа для робота. Требуется изменить ее так, чтобы узор, получающийся в конце ее работы, был таким же, но при этом при работе робота не возникало самопересечений маршрута.

Входные данные

В первой строке входного файла содержится программа для робота. Таким образом, в первой строке входного файла могут встречаться только символы E,W,N,S, а также пробельные символы, которые должны игнорироваться. Общая длина строки (включая пробельные символы) не превышает 200 символов.

Выходные данные

В выходной файл вы должны вывести одну строку с оптимизированной программой. Эта строка должна удовлетворять тем же условиям, что и входная строка.

Примеры
Входные данные
EENWSSWNN
Выходные данные
ENESWSWNN
#3583
Башня
  
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes

Петя в очередной раз купил себе набор из кубиков. На этот раз он выстроил из них настоящую крепость — последовательность из N столбиков, высота каждого столбика составляет Ai кубиков.

Вскоре ему стало интересно, насколько его крепость защищена от жуликов и воров. Для этого он ввел понятия башни. Башней называется любая последовательность из K столбиков подряд (где K — любимое число Пети). Защищенность башни определяется как суммарная высота всех столбиков этой башни (чем она больше, тем громаднее и ужаснее она кажется), умноженная на минимум высоты столбиков башни (т.к. враги, очевидно, будут пытаться проникнуть через самое слабое место башни). Неприступность крепости определяется как сумма защищенностей каждой из башен.

Петя решил как можно скорее посчитать, какова же неприступность его крепости. Однако вскоре он понял, что недостаточно знать высоту каждого из столбиков. В зависимости от того, как сгруппировать столбики в башни, получится разный результат. В различных вариантах группировки часть столбиков могут не принадлежать ни одной из башен. Разумеется, Петя выберет то разбиение на башни, при котором неприступность будет максимальна.

Петя успешно справился со своей задачей, но теперь Правительство Флатландии решило защитить свой горный курорт. Правительство уже построило крепость из кубиков (просто кубики были побольше). Теперь вы должны помочь Правительству посчитать неприступность этой крепости. Единственная трудность состоит в том, что у Правительства было очень много денег, и поэтому крепость была построена очень длинная.

Входные данные

В первой строке входного файла содержатся число N — количество столбиков в крепости и число K — любимое число Пети (1 ≤ K ≤ N ≤ 100 000). Далее на следующей строке содержатся N целых чисел, обозначающих Ai (1 ≤ Ai ≤ 106).

Выходные данные

На первой строке выведите число Q — количество башен в оптимальном разбиении. Далее выведите Q чисел — номера первых столбиков каждой башни.

Примеры
Входные данные
1 1
1
Выходные данные
1
1
Входные данные
2 1
1 1000000
Выходные данные
2
1 2
Входные данные
8 3
1 2 3 4 1 6 7 8
Выходные данные
2
2 6
Страница: 1 2 >> Отображать по:
Выбрано
:
Отменить
|
Добавить в контест