--->
9 задач
<---
Источники
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число N. Рассмотрим его разбиение на натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по невозрастанию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на натуральные слагаемые в лексикографическом порядке.
Примеры
Входные данные
5
Выходные данные
1 1 1 1 1 2 1 1 1 2 2 1 3 1 1 3 2 4 1 5
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число N. Рассмотрим его разбиение на различные натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по невозрастанию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на различные натуральные слагаемые в обратном лексикографическом порядке.
Примеры
Входные данные
5
Выходные данные
5 4 1 3 2 3 1 1 2 2 1 2 1 1 1 1 1 1 1 1
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число N. Рассмотрим его разбиение на различные натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по неубыванию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на различные натуральные слагаемые. Порядок вывода самих разбиений – лексикографический.
Примеры
Входные данные
5
Выходные данные
1 1 1 1 1 1 1 1 2 1 1 3 1 2 2 1 4 2 3 5
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Дано натуральное число N. Рассмотрим его разбиение на различные натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по неубыванию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на различные натуральные слагаемые. Слагаемые выводите по неубыванию.
Примеры
Входные данные
5
Выходные данные
5 2 3 1 4 1 2 2 1 1 3 1 1 1 2 1 1 1 1 1
#1134
Темы:
[Разбиения]
[Многоугольники. Выпуклые оболочки]
ограничение по времени на тест
1.0 second;
ограничение по памяти на тест
64 megabytes
Задачи противовоздушной обороны: ...борьба с десантом на всем маршруте пролета,
уничтожение вертолетов огневой поддержки, действующих из засады»
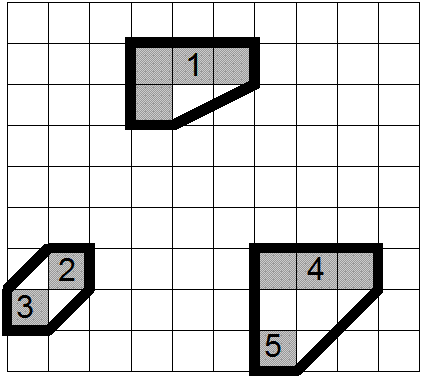Радиолокационная станция (РЛС) состоит из нескольких передатчиков (не более 5). К сожалению, их нельзя ставить рядом — они друг для друга создают помехи. Каждый передатчик состоит из квадратных модулей, которые располагаются вплотную друг к другу.
Вам дана карта района, в котором расположена РЛС. Вся карта для удобства разбита на квадраты, и для каждого квадрата известно, располагается в нем какой-то из модулей одного из передатчиков РЛС или нет.
Требуется оградить забором (или несколькими заборами) минимально возможной суммарной длины все передатчики РЛС. Забор — это произвольная ломаная (ее элементы не обязаны идти по сторонам клеток). Одним забором могут быть огорожены сразу несколько передатчиков.
Входные данные
Во входном файле записаны два числа N и M, задающие размеры района, в котором расположена РЛС (1N20, 1M20). Далее идет N строк, по M чисел в каждой, задающих карту района. Каждое из этих чисел 0 или 1 — 1 означает, что в этом квадрате находится один из модулей передатчика РЛС, а 0 — что в этом квадрате ничего ценного нет.
Общее количество передатчиков РЛС не превышает 5. Каждый передатчик — это связанная группа модулей (модули называются связанными, если они располагаются в квадратах карты, у которых есть общая граница, либо связаны через какие-то другие модули).
Ограничения на число модулей нет.
Выходные данные
В выходной файл выведите одно число — минимально возможную длину забора с тремя значащими цифрами после точки.
Примеры
Входные данные
2 2 1 0 0 1
Выходные данные
6.828
Входные данные
4 5 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1
Выходные данные
18.000
Выбрано
:
|