--->
4 задач
<---
Страница:
1
Отображать по:
#1033
Темы:
[Перебор с отсечением]
Склад конторы MacroHard представляет собой прямоугольную комнату размером NxM. На складе нарисована разметка, состоящая из линий, параллельных стенам склада, которые разбивают его на NxM квадратов 1x1.
Фирма выпускает высокотехнологичное оборудование, используемое в самых различных областях жизнедеятельности. Исторически сложилось так, что все изделия, выпускаемые этой компанией, имеют форму равнобедренного прямоугольного треугольника. При этом ассортимент изделий столь велик, что бывают изделия практически любых размеров.
Размещать изделия на складе разрешается только так, чтобы хотя бы одна сторона изделия была параллельна какой-то из стен склада, и, вдобавок, все углы изделия находились в точках пересечения линий разметки склада. Рисунки 1,2,3 иллюстрируют неправильное положение изделий, а 4,5 – правильное.
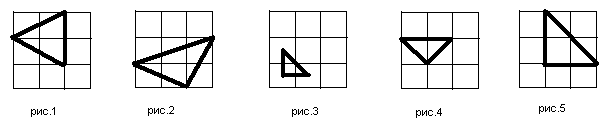
Руководство фирмы узнало, что склад планирует посетить Комиссия по неэффективному использованию складских помещений. Чтобы избежать выплаты крупного штрафа, фирма решила в срочном порядке поместить на склад изделия так, чтобы на складе не осталось свободного места. При этом было решено, что продукция, которая уже находится на складе, перемещаться не будет.
Напишите программу, которая определит, какое минимальное количество изделий можно добавить на склад, чтобы на нем не осталось свободного места.
Входные данные
В первой строке входного файла записаны три целых числа: N, M (размеры склада) и K (количество изделий, которые уже находятся на складе). Следующие K строк содержат по 6 целых чисел — координаты углов соответствующего изделия. Система координат введена так, что оси координат параллельны стенам склада и при этом один из углов склада имеет координаты (0,0), а противоположный — (N,M).
Ограничения
1N4, 1M4
Выходные данные
Первая строка выходного файла должна содержать одно число T — минимальное количество изделий, которые необходимо добавить, чтобы полностью заполнить склад. Каждая из следующих T строк должна содержать по 6 чисел — координаты углов изделий.
Примеры
Входные данные
3 2 0
Выходные данные
5 0 0 0 2 2 0 0 2 2 0 2 2 2 0 2 2 3 1 2 0 3 0 3 1 2 2 3 1 3 2
#1034
Темы:
[Перебор с отсечением]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
В связи с проведением межпланетного шашечного турнира было принято решение о строительстве орбитальной гостиницы. Она должна была представлять собой большой куб из N×N×N блоков – маленьких кубиков 1×1×1, и каждый блок должен был быть окрашен снаружи со всех сторон в какой-то один цвет. При этом некоторые блоки могли быть покрашены в один и тот же цвет.
Через год были сделаны фотографии гостиницы с каждой из 6 сторон: спереди, слева, сзади, справа, сверху, снизу. За год эксплуатации могло случиться так, что из-за непрочного крепления некоторые блоки, из которых была построена гостиница, оторвались и улетели в открытый космос. Комиссия по восстановлению гостиницы хочет по сделанным снимкам установить максимальное возможное количество оставшихся блоков.
Итак, вам необходимо по видам гостиницы (куба N×N×N, из которого, возможно, выкинуты некоторые кубики 1×1×1) с 6 сторон определить, из какого максимального количества блоков 1×1×1 она может состоять. Может оказаться так, что гостиница состоит из двух или более не связанных между собой частей.
Входные данные
В первой строке входного файла находится число N — размер гостиницы (1≤N≤10). На следующих N строках записаны виды гостиницы с 6 сторон (в следующем порядке: спереди, слева, сзади, справа, сверху, снизу). Каждый такой вид представляет собой таблицу N×N, в которой различными заглавными латинскими буквами обозначены различные цвета, а символом «.» (точка) — то, что в этом месте можно будет смотреть прямо сквозь гостиницу. Два последовательных вида отделяются друг от друга ровно одним пробелом в каждой из N строк.
Нижняя граница вида сверху соответствует верхней границе вида спереди, а верхняя граница вида снизу — нижней границе вида спереди. Для видов спереди, сзади и с боков верх и низ вида соответствуют верху и низу гостиницы.
Входные данные корректны, то есть во входном файле описано состояние, которое может получиться.
Выходные данные
Выведите в выходной файл одно число — искомое максимальное количество оставшихся блоков в гостинице.
Примеры
Входные данные
3 .R. YYR .Y. RYY .Y. .R. GRB YGR BYG RBY GYB GRB .R. YRR .Y. RRY .R. .Y.
Выходные данные
11
Входные данные
2 ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ ZZ
Выходные данные
8
#1041
Темы:
[Целые числа]
[Перебор с отсечением]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Бригада скорой помощи выехала по вызову в один из отделенных районов. К сожалению, когда диспетчер получил вызов, он успел записать только адрес дома и номер квартиры K1, а затем связь прервалась. Однако он вспомнил, что по этому же адресу дома некоторое время назад скорая помощь выезжала в квартиру K2, которая расположена в подъезда P2 на этаже N2. Известно, что в доме M этажей и количество квартир на каждой лестничной площадке одинаково. Напишите программу, которая вычилсяет номер подъезда P1 и номер этажа N1 квартиры K1.
Входные данные
Во входном файле записаны пять положительных целых чисел K1, M, K2, P2, N2. Все числа не превосходят 1000.
Выходные данные
Выведите два числа P1 и N1. Если входные данные не позволяют однозначно определить P1 или N1, вместо соответствующего числа напечатайте 0. Если входные данные противоречивы, напечатайте два числа –1 (минус один).
Примеры
Входные данные
89 20 41 1 11
Выходные данные
2 3
Входные данные
11 1 1 1 1
Выходные данные
0 1
Входные данные
3 2 2 2 1
Выходные данные
-1 -1
#1092
Темы:
[Двумерные массивы]
[Перебор с отсечением]
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes
Недавно археологической командой «Раскопай» были обнаружены остатки древней цивилизации. Особое внимание привлекла карта с месторасположением народов, живших в то время. Карта представляет собой прямоугольный лист, разлинованный горизонтальными линиями на M полос и вертикальными линиями на N столбцов. Таким образом формируются M*N клеток — древних поселений, которые заселялись сообществами. В каждой клетке этой карты написано натуральное число — идентификатор народа, к которому принадлежит это сообщество людей (рукопись с соответствием между идентификаторами и народами также была обнаружена).
<>Группа историков «Разузнай» имеет такую же карту, но только на тысячелетие древнее. Естественно, она может отличаться от той, которую нашли археологи — ведь за такой срок сообщества могли переселяться в другие поселения. Историками была высказана идея о механизме переселения народов.Чтобы объяснить этот процесс введем систему координат на карте так, что границы карты параллельны осям координат. Пусть координаты (0,0) соответствуют самой верхней левой клетке, а (N–1, M–1) — самой нижней правой. Переселение народов проходит в несколько этапов. Опишем как проходит каждый этап.
Назовем квадратом множество всех поселений с координатами (x,y) такими, что x1≤x≤x2, y1≤y≤y2, где x2–x1=y2–y1. Соответственно клетка (x1,y1) является левой верхней клеткой квадрата, (x2,y2) —нижней правой.
На каждом этапе переселения переселяются сообщества внутри некоторого квадрата по следующему правилу. Если переселение происходит внутри квадрата, левой верхней клеткой которого является клетка (x1,y1), а правой нижней — (x2,y2), то сообщество, проживавшее в поселении с координатами (x,y) (x1≤x≤x2, y1≤y≤y2) переселяется в поселение с координатами (x2–(y2–y),y2–(x2–x)), при этом, возможно, что некоторые сообщества остаются на своих местах. Все сообщества, живущие вне квадрата, в котором происходит переселение, остаются на своих местах.
Историки из «Разузнай» хотят для подтверждения (или опровержения) своей теории переселений проверить, могла ли в результате таких переселений из карты, которая есть в распоряжении «Разузнай» получиться карта, которую нашли археологи. Помогите им — напишите программу, которая будет это делать.
Входные данные
На первой строке входного файла заданы через пробел 2 натуральных числа M и N, где M — количество строк, а N — количество столбцов (1≤M≤30, 1≤N≤30). Далее описывается карта историков. После нее записана карта археологов.
Каждая карта описывается в M строках, в каждой из которых записано по N чисел — идентификаторы народов, проживающих в соответствующих поселениях. В первой строке описания записаны народы, проживающие в поселениях с координатами (0,0), (1,0), (2,0),…,(N–1,0), во второй — в поселениях (0,1), (1,1), (2,1),…,(N–1,1), в M-ой — с координатами (0, M–1), (1,M–1),…,(N–1,M–1). Идентификаторы народов — натуральные числа, не превышающие 2∙109. Некоторые идентификаторы могут не использоваться (например, на карте могут встречаться народы с номерами 1 и 3, и не встречаться народ с идентификатором 2).
Выходные данные
Если гипотеза историков подтверждается, то в выходной файл выведите количество этапов переселения народов и дальше сами эти этапы, в результате которых из карты историков получается карта археологов. Каждый этап должен быть описан четырьмя числами — x1, y1, x2, y2 (координатами углов квадрата, который переселяется). Обратите внимание, что добиваться минимального количества переселений всех народов, или же минимального количества этапов не требуется. Важно, чтобы общее число этапов не превышало 10000 (математики из общества «Докажи» доказали, что в указанных ограничениях это всегда возможно).
Если гипотеза историков неверна, т.е. из карты историков карта археологов с помощью только таких переселений получиться не могла, то выведите в выходной файл одно число –1 (минус один).
Пояснение к примеру 1
Переселение проходит в 2 этапа: на рисунке ниже закрашены квадраты, в которых происходили переселения сообществ.
Примеры
Входные данные
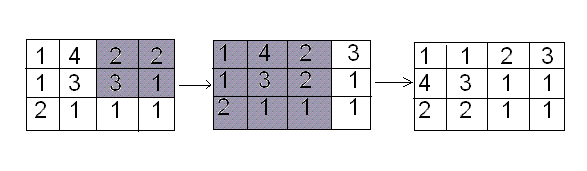
3 4 1 4 2 2 1 3 3 1 2 1 1 1 1 1 2 3 4 3 1 1 2 2 1 1
Выходные данные
2 2 0 3 1 0 0 2 2
Входные данные
2 2 6 8 5 8 6 8 5 9
Выходные данные
-1
Страница:
1
Отображать по:
Выбрано
:
|