Первый учебный день шестиклассника Пети начался с урока географии. Учитель объяснял классу, что перед тем, как изучать просторы нашей Родины, нужно научиться пользоваться географическими картами. Было также упомянуто и о том, что такое масштаб карты. В качестве домашней работы Пете и его одноклассникам задали нарисовать план (карту) своей комнаты, соблюдая масштабирование. Петю очень заинтересовало задание учителя, и поэтому, как только он пришел из школы домой, он принялся рисовать план. Это занятие было очень увлекательным, но вскоре с работы пришла Петина мама, сказала, что здоровье превыше всего и позвала его обедать. Во время обеда она по пути на кухню зашла в Петину комнату и решила, что ее надо проветрить. Для этого она открыла окно, перед которым стоял Петин стол.

Насытив свой желудок, Петя вернулся в комнату и обнаружил, что его творение сдуло ветром на пол. Сначала он обеспокоился тем, в порядке ли рисунок, но удостоверившись, что все нормально, не стал спешить и поднимать план с пола. Он вспомнил слова учителя географии, который в конце урока поведал им некое нетривиальное утверждение и предложил любопытным проверить его на досуге.

Утверждение гласило: "если взять две карты одной и той же области, сделанные с разным масштабом, и расположить меньшую поверх большей так, что меньшая карта окажется строго внутри большей, то можно найти такую точку (она называется "неподвижная точка"), что то, что изображено в этой точке на обеих картах соответствует одной и той же точке местности". Петя заметил, что пол комнаты можно считать картой комнаты (масштаб 1:1). Он решил найти неподвижную точку для лежащего на полу нарисованного им плана и пола. Но Петя не сумел сделать это самостоятельно, поэтому он обратился к вам за помощью.

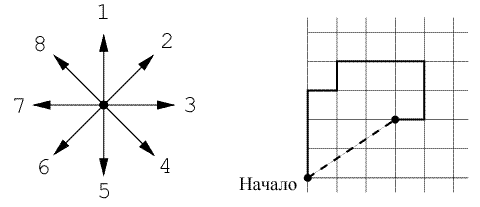
Найти закопанный пиратами клад просто: всё, что для этого нужно – это карта. Как известно, пираты обычно рисуют карты от руки и описывают алгоритм нахождения клада так: «Встаньте около одинокой пальмы. Пройдите тридцать шагов в сторону леса, потом семнадцать шагов в сторону озера, …, наконец десять шагов в сторону большого булыжника. Клад находится под ним». Большая часть таких указаний просто сводится к прохождению какого-то количества шагов в одном из восьми направлений (1 – север, 2 – северо-восток, 3 – восток, 4 – юго-восток, 5 – юг, 6 – юго-запад, 7 – запад, 8 – северо-запад) (см. рис). Длина шага в любом направлении равна 1.

Путешествие по такому пути обычно является прекрасным способом посмотреть окрестности, однако в наше время постоянной спешки ни у кого нет времени на это. Поэтому кладоискатели хотят идти напрямую в точку, где зарыт клад. Например, вместо того, чтобы проходить три шага на север, один шаг на восток, один шаг на север, три шага на восток, два шага на юг и один шаг на запад, можно пройти напрямую, использовав около 3.6 шага (см. рис).

Вам необходимо написать программу, которая по указаниям пиратов определяет точку, где зарыт клад.

Пользователь просматривает таблицу в Internet Explorer и пользуется для прокрутки изображения колесиком на мышке. При этом все изображение сдвигается вверх или вниз на T пикселов. Пользователю очень не нравится, когда курсор мыши оказывается на горизонтальных линиях, разделяющих строки таблицы. Поэтому он хочет выбрать такое положение для курсора мыши на экране, чтобы в процессе прокрутки до конца таблицы курсор как можно меньшее число раз пересекался с линиями таблицы.

При этом если в каком-то положении курсор оказывается на двух линиях таблицы, то это считается за два пересечения курсора с линиями таблицы. Если какую-то линию курсор мыши пересекает в двух положениях (то есть, например, высота курсора 10 пикселей, а при прокрутке таблица сдвигается на 7 пикселей, тогда курсор мыши может оказываться на одной линии в двух состояниях прокрутки), то это также считается за два пересечения.

Экран монитора имеет разрешение по вертикали U пикселей. Координаты введены так, что самые верхние точки экрана имеют координату 0, а нижние — координату U–1.

Курсор мыши имеет высоту H пикселов. Расположением курсора считается самая верхняя точка курсора. Таким образом, если мы говорим, что он расположен, например, в точке с координатами 0 на экране, то его изображение расположено в точках с координатами от 0 до H–1. Курсор мыши всегда целиком помещается на экране, то есть допустимыми координатами для его расположения являются координаты от 0 до U–H.>

Таблица, которую просматривает пользователь, имеет высоту L пикселов и состоит из N­–1 строки, и, следовательно, в ней N горизонтальных линий, которые имеют координаты X₁, X₂, …, X_N. При этом 0=X₁<X₂<X₃<…<X_N=L–1.

В начальный момент времени таблица расположена так, что линия, имеющая координату 0 в таблице отображается в 0-й строке пикселов монитора. Далее при прокрутке таблица каждый раз сдвигается на T пикселов (то есть в 0-й строке монитора оказывается строка пикселов, имеющая в таблице координату T, координату 2T и т.д.). Так происходит до тех пор, пока на экране не окажется нижняя линия таблицы (которая имеет координату X_N). После этого дальнейшая прокрутка не происходит (если изначально X_N<U, то прокрутка вообще не происходит).

Будем говорить, что для наблюдателя лес является дремучим, если из своего текущего положения наблюдатель видит только деревья. Вам дана карта леса и координаты точки, в которой находится наблюдатель. Требуется определить, кажется ли лес дремучим данному наблюдателю.

На карте леса все деревья изображаются кругами. При этом в лесу бывают сросшиеся деревья (изображения таких деревьев на карте пересекаются), также одно дерево может находиться внутри другого. Точка, в которой стоит наблюдатель, не лежит внутри или на границе ни одного из деревьев.

В пространстве с прямоугольной системой координат находятся два куба. Про них известно следующее:

• сторона каждого куба равна 2,
• центр (т.е. центр симметрии) каждого куба совпадает с началом данной системы координат,
• координаты вершин >первого куба A₁A₂A₃A₄A₅A₆A₇A₈ следующие: A₁(1, 1, 1), A₂(1, –1, 1), A₃(–1, –1, 1), A₄(–1, 1, 1), A₅(1, 1, –1), A₆(1, –1, –1), A₇(–1, –1, –1), A₈(–1, 1, –1),
• вершины второго куба B₁B₂B₃B₄B₅B₆B₇B₈ пронумерованы так, что путем поворота кубы можно совместить, и при этом совместятся соответствующие их вершины (A₁ и B₁, A₂ и B₂, … , A₈ и B₈)
• координаты вершин второго куба даны во входном файле.

Требуется найти объем пересечения (т.е. общей части) этих кубов.