Турнир Архимеда(52 задач)
Кировские командные турниры(8 задач)
Барнаульские командные турниры(10 задач)
Московская командная олимпиада(246 задач)
Командные чемпионаты школьников Санкт-Петербурга по программированию(167 задач)
ВКОШП(180 задач)
На плоскости нарисовали прямоугольник, после чего его разрезали прямыми. Напишите программу, которая вычислит, сколько из полученных кусков исходного прямоугольника имеют треугольную форму.
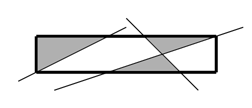
Рисунок, соответствующий 1-му примеру входных и выходных данных
Сначала на вход программы поступают два положительных числа X и Y, задающих координаты правого верхнего угла прямоугольника. Прямоугольник расположен в системе координат так, что левый нижний его угол имеет координаты 0,0 и стороны параллельны осям координат.
Далее вводится целое число N — количество разрезов (1≤N≤200). Затем описываются сами разрезы. Каждый разрез делался вдоль некоторой прямой. Каждая прямая, соответствующая разрезу, задается тремя числами A, B, C такими, что все точки (x,y) этой прямой (и только они) удовлетворяют уравнению Ax+By+C=0 (при этом всегда A2+B2>0).
Все входные данные (кроме N) – вещественные числа, заданы с двумя знаками после десятичной точки и не превышают 104. Никакие две прямые не совпадают между собой и не содержат сторон прямоугольника. Каждый разрез проходит через точки внутри исходного прямоугольника.
Выведите одно целое число — количество частей исходного прямоугольника, имеющих треугольную форму.
Система оценки
1 балл получат программы, правильно решающие задачу при ограничении 1≤N≤50.
5.00 1.00 3 1.00 -2.00 0.00 1.00 -3.00 -2.00 1.00 1.00 -4.00
3
4.00 2.00 2 1.00 -2.00 0.00 1.00 2.00 -4.00
4
При игре в лапту одна команда ловит мяч и пытается осалить им бегущего. Игрок другой команды должен, перед тем как бежать, ударить мяч в поле. Известно, на какое максимальное расстояние он может ударить, а также скорости и начальные координаты игроков другой команды. Требуется выбрать направление и силу удара так, чтобы минимальное время, которое потребуется другой команде, чтобы поднять мяч с земли, было наибольшим. (Пока мяч летит, игроки стоят на местах.)
В первой строке входных данных содержатся два числа: D — максимальное расстояние удара и N — количество соперников на поле (D и N натуральные числа, D ≤ 1000, N ≤ 200). В следующих N строках задается по три числа – начальные координаты xi и yi и максимальная скорость vi соответствующего игрока (скорости и координаты — целые числа, –1000 ≤ xi ≤ 1000, 0 ≤ yi ≤ 1000, 0 < vi ≤ 1000), никакие два игрока не находятся изначально в одной точке. Игрок, бьющий мяч, находится в точке с координатами (0,0). Мяч выбивается в точку с неотрицательной ординатой (y ≥ 0).
Выведите сначала время, которое потребуется игрокам, чтобы добежать до мяча, а затем координаты точки, в которую нужно выбить мяч. Если таких точек несколько, выведите координаты любой из них. Время и координаты нужно вывести с точностью 10–3.
Оценка задачи
1 балл получат программы, которые верно работают, когда в поле не более двух соперников.
10 2 1 1 1 -1 1 1
9.05539 0.00000 10.00000
Картины художников-абстракционистов весьма необычны. На них часто изображены абсолютно непонятные предметы. Один известный художник-абстракционист решил добавить своим картинам оригинальности следующим способом. Вместо прямоугольных рамок, в которые обычно вставляются картины, он решил на ближайшей выставке использовать треугольные.
Однако все оказалось совсем не так просто. Художник изготовил рамку, поместил в нее картину и понял, что что-то не так. Рамка получилась слишком широкой, и картина выглядела совсем не так ярко, как он ожидал.
Немного поразмыслив, художник понял, что то, насколько рамка «подходит» для картины, определяется площадью рамки. Кроме этого он понял, что рамки надо не изготавливать самостоятельно, а покупать в специальном магазине. Заглянув в прайс-лист магазина, он увидел, что для каждой рамки в нем указаны длины внешних сторон и ширина.
Поясним подробнее то, как выглядит треугольная рамка. Ее изготовление происходит следующим образом: берется доска из красного дерева, имеющая форму треугольника со сторонами a, b и c. После этого стороны этого треугольника мысленно сдвигаются внутрь него на расстояние d (измеряемое по перпендикуляру к соответствующей стороне). На точках пересечения «сдвинутых» сторон строится маленький треугольник, который затем вырезается из исходного. Пример рамки со сторонами a = 6, b = 8, c = 10 и шириной d = 1 показан на рисунке.

Помогите художнику по имеющимся в прайс-листе данным вычислить площадь рамки.
На вход программы поступают четыре целых числа a, b, c, d ( 1![]() a, b, c, d
a, b, c, d![]() 1000) – длины внешних сторон рамки и ее ширина, соответственно. Гарантируется, что треугольник со сторонами a, b и c существует, и что в треугольнике есть точка, расстояние от которой до ближайшей стороны строго больше d.
1000) – длины внешних сторон рамки и ее ширина, соответственно. Гарантируется, что треугольник со сторонами a, b и c существует, и что в треугольнике есть точка, расстояние от которой до ближайшей стороны строго больше d.
Выведите площадь рамки с точностью не меньше 10-5.
6 8 10 1
18.0
Во Флатландии n городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание n - 1 шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды – числа от 1 до n.
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача – таким образом сопоставить числам от 1 до n города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
В первой строке вводится целое число n – количество городов во Флатландии ( 2![]() n
n![]() 1500).
1500).
Далее следует n описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города – строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа x и y – координаты города. Координаты не превышают 104 по абсолютной величине.
Далее следуют n - 1 строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа – номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более, чем одним шоссе.
Выведите n строк, i-я из этих строк должна содержать название города, который следует сопоставить числу i в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите строку «No solution».
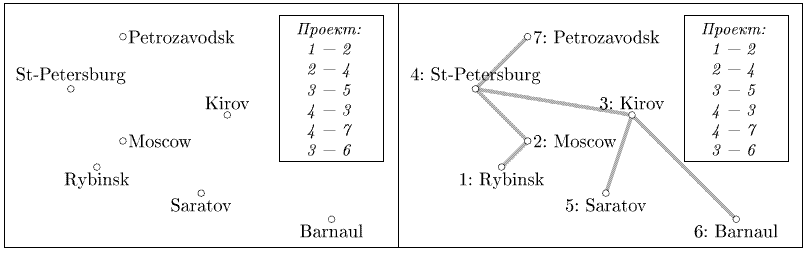
7 Moscow 2 2 St-Petersburg 0 4 Kirov 6 3 Saratov 5 0 Rybinsk 1 1 Petrozavodsk 2 6 Barnaul 10 -1 1 2 2 4 3 5 4 3 4 7 3 6
St-Petersburg Rybinsk Kirov Saratov Moscow Petrozavodsk Barnaul
Одной из первоочередных задач, стоящих перед министерством обороны Флатландии, является модернизация вооружения. В связи с этим было решено построить новый испытательный полигон.
По форме полигон представляет собой выпуклый многоугольник. Для демонстрации военных испытаний на полигоне различным чиновникам, неподалеку от него решено было построить наблюдательный центр. В результате длительных исследований было установлено, что основной характеристикой местоположения наблюдательного центра является степень этого центра относительно полигона.
Степень точки A относительно многоугольника вычисляется по следующему правилу. Рассмотрим все лучи с вершиной в точке A, имеющие общие точки с многоугольником. Для каждого такого луча найдем минимальное и максимальное расстояние вдоль него от точки A до некоторой точки многоугольника: dmin и dmax. Степенью точки относительно данного многоугольника назовем минимум величины dmin×dmax по всем таким лучам.
Военные не справляются с задачей вычисления степени наблюдательного центра относительно полигона и решили подключить к этой задаче вас. Помогите им!
Будем считать, что наблюдательный центр находится в точке (0, 0). На вход программы поступает описание полигона.
В первой строке вводится число n – количество вершин полигона ( 3![]() n
n![]() 100). Следующие n строк содержат по два вещественных числа – координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают 1000 по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
100). Следующие n строк содержат по два вещественных числа – координаты вершин полигона в порядке обхода их против часовой стрелки. Координаты не превышают 1000 по абсолютной величине. Гарантируется, что наблюдательный центр находится вне полигона, полигон представляет собой выпуклый невырожденный многоугольник, никакие три его последовательных вершины не лежат на одной прямой. Никакая сторона многоугольника не лежит на луче с центром в начале координат.
Выведите одно число – степень наблюдательного центра относительно полигона. Ответ должен отличаться от правильного не более чем на 10-4.
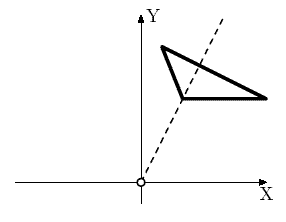
3 1.0 2.0 3.0 2.0 0.5 3.25
7.0000000000