#1340

Темы: [Остатки] [Перебор с отсечением] [Жадный алгоритм]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Заключительный этап, 2009, Задача D ]

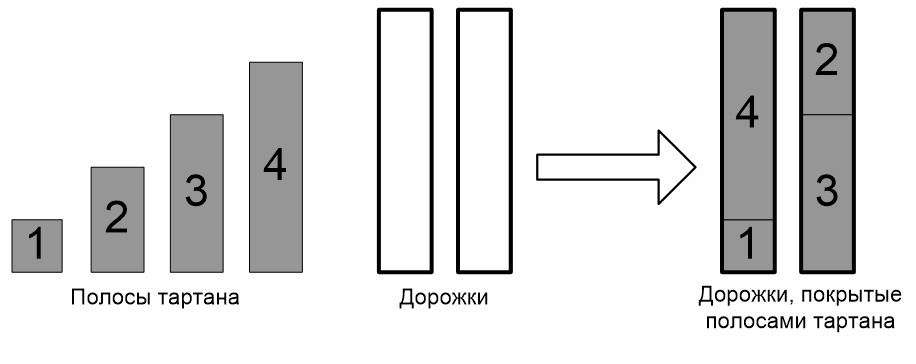
В стране Флатландия решили построить легкоатлетический манеж с M одинаковыми прямолинейными беговыми дорожками. Они будут покрыты полосами из синтетического материала пружинкин. На складе имеются N полос пружинкина, длины которых равны 1, 2, …, N метров соответственно (i-я полоса имеет длину i метров).

Было решено использовать все полосы со склада, что определило длину дорожек манежа. Полосы пружинкина должны быть уложены без перекрытий и промежутков. Разрезать полосы на части нельзя. Полосы укладываются вдоль дорожек, ширина полосы пружинкина совпадает с шириной беговой дорожки.

Требуется написать программу, которая определяет, можно ли покрыть всем имеющимся материалом M дорожек, и если это возможно, то распределяет полосы пружинкина по дорожкам.

Входные данные

Во входном файле содержатся два целых числа, разделенных пробелом: M — количество дорожек и N — количество полос пружинкина (1 ≤ M ≤ 1000, 1 ≤ N ≤ 30000).

Выходные данные

В случае, если распределить имеющиеся полосы пружинкина на M дорожек одинаковой длины невозможно, то в выходной файл выведите слово «NO».

В противном случае, в первую строку выведите слово «YES». В последующих M строках дайте описание использованных полос для каждой дорожки в следующем формате: сначала целое число t — количество полос на дорожке, затем t целых чисел — длины полос, которые составят эту дорожку. Если решений несколько, можно вывести любое из них.

В задаче есть группа на первые 17 тестов и она оценивается в 20 баллов. затем идёт потестовая оценка по 2 балла за пройденный тест.

Примеры входных и выходных данных

Ввод

Вывод

2 4

YES

2 1 4

2 3 2

3 4

NO

#3182

Колесо Фортуны

Темы: [Линейный поиск] [Остатки]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2011, 1 день, Задача B ]

Развлекательный телеканал транслирует шоу «Колесо Фортуны». В процессе игры участники шоу крутят большое колесо, разделенное на сектора. В каждом секторе этого колеса записано число. После того как колесо останавливается, специальная стрелка указывает на один из секторов. Число в этом секторе определяет выигрыш игрока.

Юный участник шоу заметил, что колесо в процессе вращения замедляется из-за того, что стрелка задевает за выступы на колесе, находящиеся между секторами. Если колесо вращается с угловой скоростью \(v\) градусов в секунду, и стрелка, переходя из сектора \(X\) к следующему сектору, задевает за очередной выступ, то текущая угловая скорость движения колеса уменьшается на \(k\) градусов в секунду. При этом если \(v \le k\), то колесо не может преодолеть препятствие и останавливается. Стрелка в этом случае будет указывать на сектор \(X\).

Юный участник шоу собирается вращать колесо. Зная порядок секторов на колесе, он хочет заставить колесо вращаться с такой начальной скоростью, чтобы после остановки колеса стрелка указала на как можно большее число. Колесо можно вращать в любом направлении и придавать ему начальную угловую скорость от \(a\) до \(b\) градусов в секунду.

Требуется написать программу, которая по заданному расположению чисел в секторах, минимальной и максимальной начальной угловой скорости вращения колеса и величине замедления колеса при переходе через границу секторов вычисляет максимальный выигрыш.

Входные данные

Первая строка входного файла содержит целое число \(n\) — количество секторов колеса (\(3 \le n \le 100\)).

Вторая строка входного файла содержит \(n\) положительных целых чисел, каждое из которых не превышает \(1000\) — числа, записанные в секторах колеса. Числа приведены в порядке следования секторов по часовой стрелке. Изначально стрелка указывает на первое число.

Третья строка содержит три целых числа: \(a\), \(b\) и \(k\) (\(1 \le a \le b \le 10^9\), \(1 \le k \le 10^9\)).

Выходные данные

В выходном файле должно содержаться одно целое число — максимальный выигрыш.

Примечание

В первом примере возможны следующие варианты: можно придать начальную скорость колесу равную 3 или 4, что приведет к тому, что стрелка преодолеет одну границу между секторами, или придать начальную скорость равную 5, что позволит стрелке преодолеть 2 границы между секторами. В первом варианте, если закрутить колесо в одну сторону, то выигрыш получится равным 2, а если закрутить его в противоположную сторону, то — 5. Во втором варианте, если закрутить колесо в одну сторону, то выигрыш будет равным 3, а если в другую сторону, то — 4.

Во втором примере возможна только одна начальная скорость вращения колеса — 15 градусов в секунду. В этом случае при вращении колеса стрелка преодолеет семь границ между секторами. Тогда если его закрутить в одном направлении, то выигрыш составит 4, а если в противоположном направлении, то — 3.

Наконец, в третьем примере оптимальная начальная скорость вращения колеса равна 2 градусам в секунду. В этом случае стрелка вообще не сможет преодолеть границу между секторами, и выигрыш будет равен 5.

Правильные решения для тестов, в которых \(1 \le a \le b \le 1000\), будут оцениваться из 50 баллов.

Примеры

Входные данные

5
1 2 3 4 5
3 5 2

Выходные данные

Входные данные

5
1 2 3 4 5
15 15 2

Выходные данные

Входные данные

5
5 4 3 2 1
2 5 2

Выходные данные

#113100

Три сына

Темы: [Остатки] [Конструктив]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2016, 2 день, Три сына ] [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2016, 2 день, Задача A ]

Во владениях короля Флатландии находится прямая дорога длиной \(n\) километров, по одну сторону от которой расположен огромный лесной массив. Король Флатландии проникся идеями защиты природы и решил превратить свой лесной массив в заповедник. Но сыновья стали сопротивляться: ведь им хотелось получить эти земли в наследство.

У короля три сына: младший, средний и старший. Король решил, что в заповедник не войдут участки лесного массива, которые он оставит сыновьям в наследство. При составлении завещания король хочет, чтобы для участков выполнялись следующие условия:

каждый участок должен иметь форму квадрата, длина стороны которого выражается целым положительным числом. Одна из сторон каждого квадрата должна лежать на дороге. Пусть участки имеют размеры \(a \times a, b \times b\) и \(c \times c\);
стороны квадратов должны полностью покрывать дорогу: величина a + b + c должна быть равна \(n\);
участок младшего сына должен быть строго меньше участка среднего сына, а участок среднего сына должен, в свою очередь, быть строго меньше участка старшего сына, то есть должно выполняться неравенство \(a < b < c\);
суммарная площадь участков \(a^2 + b^2+ c^2\) должна быть минимальна.

Требуется написать программу, которая по заданной длине дороги определяет размеры участков, которые следует выделить сыновьям короля.

Входные данные

Входной файл содержит одно целое число \(n\) (\(6 \le n \le 10^9\) ).

Выходные данные

Выходной файл должен содержать три целых положительных числа, разделенных пробелами: \(a\), \(b\) и \(c\) – длины сторон участков, которые следует выделить младшему, среднему и старшему сыну, соответственно. Если оптимальных решений несколько, разрешается вывести любое.

Пояснение к примеру

Описание подзадач и системы оценивания

В этой задаче четыре подзадачи. Баллы за подзадачу начисляются только в случае, если все тесты для данной подзадачи пройдены.

Подзадача 1 (25 баллов)

\(n \le 50\)

Подзадача 2 (25 баллов)

\(n \le 2000\)

Подзадача 3 (25 баллов)

\(n \le 40000\)

Подзадача 4 (25 баллов)

\(n \le 10^9\)

Примеры

Входные данные

Выходные данные

1 2 3