#721

Шнурки

Темы: [Целые числа]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2007, Задача A ]

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N.

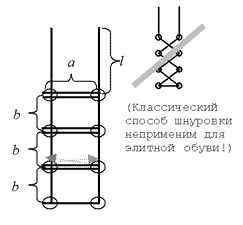Рис. 1 Шнуровка должна происходить элитным способом «наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.» (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l.

Какова должна быть длина шнурка для этих ботинок?

Входные данные

Вводятся четыре натуральных числа a, b, l и N.

Выходные данные

Ваша программа должна выводить одно число – искомую длину шнурка.

Примеры

Входные данные

2 1 3 4

Выходные данные

#1178

Оплата интернета

Темы: [Целые числа] [Условный оператор (if)]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2008, Задача A ]

Витя подключен к интернет по следующему тарифному плану. Ежемесячная абонентская плата составляет A рублей, и в эту абонентскую плату включено B мегабайт трафика. Неизрасходованные мегабайты в конце месяца «сгорают». Если трафик превышает B мегабайт, то каждый мегабайт трафика сверх предоплаченных стоит C рублей.

Известно, что за прошлый месяц Витя израсходовал D мегабайт трафика. Определите, во сколько обошелся ему доступ в интернет в прошлом месяце (считая в том числе и абонентскую плату)?

Входные данные

Вводятся четыре натуральных числа A, B, C, D. Все числа не превышают 100.

Выходные данные

Выведите одно число — сумму (в рублях), которую Витя должен заплатить за интернет.

Примеры

Входные данные

100 10 12 15

Выходные данные

Входные данные

100 10 12 1

Выходные данные

#1835

Конец K-ого урока

Темы: [Задачи на моделирование] [Целые числа]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2009, Задача A ]

В школе продолжительность каждого урока 45 минут, а перемены между уроками – всего 5 минут. Первый урок начинается ровно в 8 часов утра. Напишите программу, отвечающую на вопрос «во сколько в этой школе заканчивается \(K\)-ый урок?»

Входные данные

Вводится одно натуральное число \(K\), не превышающее 15.

Выходные данные

Выведите время окончания \(K\)-ого урока: сначала часы, потом минуты, разделяя их пробелом.

Примеры

Входные данные

Выходные данные

8 45

Входные данные

Выходные данные

12 55

#3014

Поклейка обоев

Темы: [Целые числа]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Муниципальный этап, Москва, 2010, Задача A ]

Пете нужно оклеить обоями стену размером N метров в высоту и M метров в ширину. Для поклейки используются обои, которые продаются рулонами. Каждый рулон имеет ширину 1 метр и длину K метров. Обои клеятся на стену вертикальными полосами (сверху вниз). При этом Петя хочет так поклеить обои, чтобы горизонтальных стыков разных кусков не было (то есть один цельный кусок клеится от потолка до пола). От рулона можно отрезать куски нужного размера (иногда при этом может оставаться кусок, меньшего размера, который поэтому не может быть поклеен, этот кусок идет в отходы).

По данным числам N, M и K определите наименьшее количество рулонов, которое нужно купить Пете, чтобы оклеить всю стену.

Входные данные

Вводятся натуральные числа N, M и K (1 ≤ N ≤ 100, 1 ≤ M ≤ 100, N ≤K ≤100).

Выходные данные

Выведите одно число - количество рулонов, которые должен купить Петя.

Примеры

Входные данные

10
5
25

Выходные данные

Входные данные

3
6
9

Выходные данные

#3864

Цапли

Темы: [Целые числа]

Источники: [ Личные олимпиады, Всероссийская олимпиада школьников, Региональный этап, 2012, 1 день, Задача A ]

Петя и Маша пришли в зоопарк. Больше всего Пете понравились цапли. Он был поражен их способностью спать на одной ноге.

В вольере находятся несколько цапель. Некоторые из них стоят на двух ногах, некоторые — на одной. Когда цапля стоит на одной ноге, то другую ее ногу не видно. Петя пересчитал видимые ноги всех цапель, и у него получилось число a.

Через несколько минут к вольеру подошла Маша. За это время некоторые цапли могли поменять позу, поэтому Петя предложил ей заново пересчитать видимые ноги цапель. Когда Маша это сделала, у нее получилось число b.

Выйдя из зоопарка, Петя с Машей заинтересовались, сколько же всего цапель было в вольере. Вскоре ребята поняли, что однозначно определить это число можно не всегда. Теперь они хотят понять, какое минимальное и какое максимальное количество цапель могло быть в вольере.

Требуется написать программу, которая по заданным числам a и b выведет минимальное и максимальное количество цапель, которое могло быть в вольере.

Входные данные

Входной файл содержит два целых числа a и b, разделенных ровно одним пробелом (1 ≤ a ≤ 10⁹, 1 ≤ b ≤ 10⁹).

Выходные данные

Выведите в выходной файл два целых числа, разделенных пробелом — минимальное и максимальное число цапель, которое могло быть в вольере. Гарантируется, что хотя бы одно количество цапель соответствует условию задачи.

Примечание к примеру тестов

В приведенном примере возможны следующие варианты:

В вольере две цапли. Когда Петя считал ноги, одна цапля стояла на двух ногах, а другая — на одной. Петя насчитал три ноги. Когда Маша считала ноги, обе цапли стояли на двух ногах, Маша насчитала четыре ноги.
В вольере три цапли. Когда Петя считал ноги, все цапли стояли на одной ноге, Петя насчитал три ноги. Когда Маша считала ноги, одна цапля стояла на двух ногах, а еще две — на одной. Маша насчитала четыре ноги.

Примеры

Входные данные

3 4

Выходные данные

2 3