Темы --> Информатика --> Алгоритмы --> Вычислительная геометрия --> Элементарная геометрия
---> 7 задач <---
Источники --> Личные олимпиады --> Всероссийская олимпиада школьников
    Муниципальный этап(80 задач)
    Окружная олимпиада(18 задач)
    Региональный этап(109 задач)
    Заключительный этап(97 задач)
Страница: << 1 2 Отображать по:
#3870
Космический кегельбан
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
256 megabytes

На планете Плюк открылся новый космический кегельбан. Поле для кегельбана представляет собой бесконечную плоскость, на которой расставлены кегли.

Каждая кегля представляет собой высокий цилиндр с основанием в виде круга радиусом r метров. Все кегли одинаковые. Кегли расставлены по следующим правилам. Кегли образуют n рядов, в первом ряду стоит одна кегля, во втором — две, и так далее. В последнем n-м ряду стоит n кеглей. Введем на плоскости систему координат таким образом, чтобы единица измерения была равна одному километру. Центр единственной кегли в первом ряду находится в точке (0, 0). Центры кеглей во втором ряду находятся в точках (–1, 1) и (1, 1). Таким образом, центры кеглей в i-м ряду находятся в точках с координатами (–(i – 1), i –  1), (–( i – 3), i – 1), …, (i – 1, i – 1).

Игра происходит следующим образом. Используется шар с радиусом q метров. Игрок выбирает начальное положение центра шара (xc,  yc) и вектор направления движения шара (vx, vy). После этого шар помещается в начальную точку и двигается, не останавливаясь, в направлении вектора (vx, vy). Считается, что шар сбил кеглю, если в процессе движения шара имеет место ситуация, когда у шара и кегли есть общая точка. Сбитые кегли не меняют направления движения шара и не сбивают соседние кегли при падении.

На рисунке приведен пример расположения кеглей для r = 500, n = 4 и шара для q = 1000, xc = –2, yc = –2, vx = 1, vy = 1.

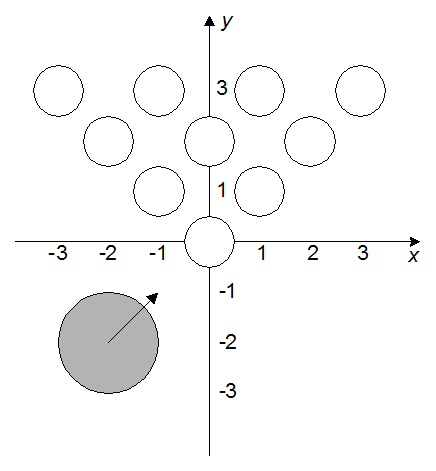
Требуется написать программу, которая по заданным радиусу кегли r, количеству рядов кеглей n, радиусу шара q, его начальному положению ( xc, yc) и вектору направления движения (vx,  vy) определяет количество кеглей, сбитых шаром.

Входные данные

Первая строка входного файла содержит два целых числа: r и n, разделенных ровно одним пробелом (1 ≤ r ≤ 700, 1  ≤ n ≤ 200 000).

Вторая строка входного файла содержит целое число q (1  ≤ q ≤ 109).

Третья строка входного файла содержит два целых числа xc и yc, разделенных ровно одним пробелом (–106≤ xc ≤ 106, –10 6≤ yc, 1000 ×yc < –(r + q) ).

Четвертая строка входного файла содержит два целых числа vx и vy, разделенных ровно одним пробелом (–106≤ vx ≤ 106, 0  < vy ≤ 106).

Выходные данные

Выходной файл должен содержать одно целое число — количество сбитых кеглей.

Примечание

Рисунок ниже показывает, какие кегли будут сбиты (такие кегли обозначены «х»).

Система оценки

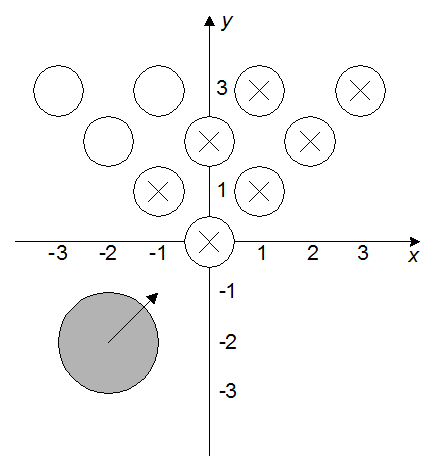
Потестовая.

Примеры
Входные данные
500 4
1000
-2 -2
1 1
Выходные данные
7
#111494
Две окружности
  
ограничение по времени на тест
2.0 second;
ограничение по памяти на тест
64 megabytes

Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью небольших камушков. Митя разложил на поле n камушков так, чтобы каждый из них находился на одной из окружностей или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности размещался хотя бы один камушек. Обладая великолепным глазомером, Митя расположил камушки на окружностях абсолютно точно, без какой-либо погрешности.

На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем которого он был, то есть, восстановить окружности.

Требуется написать программу, которая по координатам камушков на поле находит вариант размещения их на двух несовпадающих окружностях.

Входные данные

Первая строка входного файла содержит целое число n — количество размещенных Митей камушков на поле (\(2 \leq n \leq 2000\)). Последующие n строк содержат целочисленные координаты (\(x_i\), \(y_i\)) камушков — по одной паре координат, разделенных пробелом, в каждой строке (\(−10^6 \leq x_i, y_i \leq 10^6\)). Никакие два камушка не размещаются в одной точке.

Гарантируется, что ответ для заданного набора камушков существует.

Выходные данные

Выходной файл должен содержать две строки. Первая строка должна содержать последовательность номеров всех камушков, которые принадлежат первой окружности, вторая строка — последовательность номеров всех камушков, которые принадлежат второй окружности.

Каждый камушек должен встречаться хотя бы в одной из двух последовательностей. Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей. Считается, что камушки пронумерованы от 1 до n в порядке их следования во входных данных.

Нумерация окружностей не имеет значения, то есть выводить две последовательности можно в любом порядке. Числа в последовательностях можно также выводить в произвольном порядке. Каждая из последовательностей должна содержать не менее одного числа. Все числа в строках должны быть разделены пробелами.

Если вариантов расположения окружностей несколько, можно выбрать любой из них.

Система оценивания

Правильные решения для тестов, в которых 2 ≤ n ≤ 50, будут оцениваться из 50 баллов.

Примеры
Входные данные
7
1 -1
0 0
1 1
3 1
3 -1
2 0
4 0
Выходные данные
1 2 3 6 
4 5 6 7
Входные данные
5
-1000000 0
0 1000000
1000000 0
0 -1000000
0 0
Выходные данные
1 2 3 4 
5
Страница: << 1 2 Отображать по:
Выбрано
:
Отменить
|
Добавить в контест