2010(8 задач)
2011(8 задач)
2012(8 задач)
2013(8 задач)
2014(8 задач)
2015(8 задач)
2016(8 задач)
2017(8 задач)
Московская областная олимпиада(13 задач)
Кировская открытая областная олимпиада(21 задач)
Санкт-Петербург(3 задач)
Юный футболист Митя обнаружил на школьном футбольном поле две различные окружности, нарисованные едва заметной белой краской. Вспомнив истории о загадочных кругах на полях, он отметил эти окружности с помощью небольших камушков. Митя разложил на поле n камушков так, чтобы каждый из них находился на одной из окружностей или даже на их пересечении, если эти окружности пересекаются. Получилось так, что на каждой окружности размещался хотя бы один камушек. Обладая великолепным глазомером, Митя расположил камушки на окружностях абсолютно точно, без какой-либо погрешности.
На следующий день пошел дождь, краска стерлась, и нарисованные окружности исчезли, но все камушки остались на своих местах. Теперь Мите очень нужно найти доказательство необычного явления, свидетелем которого он был, то есть, восстановить окружности.
Требуется написать программу, которая по координатам камушков на поле находит вариант размещения их на двух несовпадающих окружностях.
Первая строка входного файла содержит целое число n — количество размещенных Митей камушков на поле (\(2 \leq n \leq 2000\)). Последующие n строк содержат целочисленные координаты (\(x_i\), \(y_i\)) камушков — по одной паре координат, разделенных пробелом, в каждой строке (\(−10^6 \leq x_i, y_i \leq 10^6\)). Никакие два камушка не размещаются в одной точке.
Гарантируется, что ответ для заданного набора камушков существует.
Выходной файл должен содержать две строки. Первая строка должна содержать последовательность номеров всех камушков, которые принадлежат первой окружности, вторая строка — последовательность номеров всех камушков, которые принадлежат второй окружности.
Каждый камушек должен встречаться хотя бы в одной из двух последовательностей. Если камушек встречается в обеих последовательностях, то это обозначает, что он находится на пересечении окружностей. Считается, что камушки пронумерованы от 1 до n в порядке их следования во входных данных.
Нумерация окружностей не имеет значения, то есть выводить две последовательности можно в любом порядке. Числа в последовательностях можно также выводить в произвольном порядке. Каждая из последовательностей должна содержать не менее одного числа. Все числа в строках должны быть разделены пробелами.
Если вариантов расположения окружностей несколько, можно выбрать любой из них.
Правильные решения для тестов, в которых 2 ≤ n ≤ 50, будут оцениваться из 50 баллов.
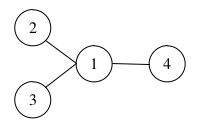
7 1 -1 0 0 1 1 3 1 3 -1 2 0 4 0
1 2 3 6 4 5 6 7
5 -1000000 0 0 1000000 1000000 0 0 -1000000 0 0
1 2 3 4 5
В стране Триландии близятся выборы новых столиц. Столицы в Триландии необычные, поскольку ими являются одновременно сразу три различных города. Такая идея размещения столиц основана на исследованиях эффективности управления страной, выполненных ведущими экономистами Триландии.
Всего в Триландии n городов, из которых некоторые пары городов соединены дорогами, и по каждой из них можно проехать в обе стороны. Время проезда по каждой дороге в одну сторону равно одному часу. При этом все города соединены дорогами таким образом, что из каждого города можно добраться в любой другой, причем это можно сделать единственным способом, если по каждой дороге проезжать не более одного раза и только в одну сторону.
Как показали результаты проведенных триландскими экономистами исследований, управление страной будет наиболее эффективным, если три столицы будут выбраны так, что время кратчайшего пути между каждой парой столиц составит ровно d часов. Перед проведением выборов необходимо знать, сколько существует различных троек городов, удовлетворяющих описанным выше свойствам. Две тройки городов считаются различными, если в первой тройке есть хотя бы один город, которого нет во второй тройке, и наоборот.
Требуется написать программу, которая по количеству городов в Триландии и описанию дорог находит количество троек городов, которые могут быть столицами.
Первая строка входного файла содержит два разделенных пробелом целых числа: количество городов в Триландии n и требуемое время в пути между столицами d (\(3 \leq n \leq 10^5\), \(1 \leq d < n\)). Каждая из последующих (n – 1) строк содержит описание одной дороги: пару разделенных пробелом различных целых чисел \(a_i\) и \(b_i\) — номера городов, которые соединены двусторонней дорогой (\(1 \leq a_i \leq n\), \(1 \leq b_i \leq n\), \(a_i \ne b_i\)). Каждая пара городов соединена не более чем одной дорогой.
Выходной файл должен содержать одно целое число — количество подходящих троек городов, которые могут быть выбраны столицами. В случае, если нужных троек городов не окажется, выходной файл должен содержать ноль.
В первом примере существует единственный способ выбрать три столицы: города под номерами 2, 3 и 4. Рисунок, соответствующий первому примеру, приведен ниже.
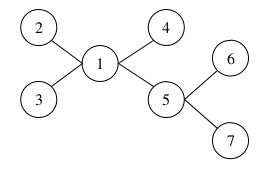
Во втором примере существует четыре варианта выбора трёх столиц из четверки городов: 2, 3, 4 и 5. Можно также выбрать столицами города с номерами 1, 6 и 7. Рисунок, соответствующий второму примеру, приведен ниже.
Правильные решения для тестов, в которых 3 ≤ n ≤ 50, будут оцениваться из 20 баллов.
Правильные решения для тестов, в которых 3 ≤ n ≤ 500, будут оцениваться из 40 баллов.
Правильные решения для тестов, в которых 3 ≤ n ≤ 5000, будут оцениваться из 60 баллов.
4 2 1 2 1 3 1 4
1
7 2 1 2 1 3 1 4 5 1 5 6 5 7
5
Длина катета каждого из представленных выше треугольников равна одному сантиметру. За один такт видеокарта не может отобразить более чем \(a_i\) треугольников \(i\)-того типа.
Необходимо определить максимально возможную длину стороны квадрата, который может быть изображен видеокартой на экране монитора за один такт. При этом квадрат должен быть расположен так, чтобы его стороны были параллельны краям монитора.
Требуется написать программу, которая решает поставленную задачу.
Первая строка входного файла содержит разделенные пробелами четыре целых числа: \(a_1\), \(a_2\), \(a_3\), \(a_4\) (0 ≤ \(a_1\), \(a_2\), \(a_3\), \(a_4\) ≤ 1018). Входные данные могут превышать максимальные значения для 32 битного типа данных.
Выходной файл должен содержать одно число – максимально возможную длину стороны квадрата.
Далее приведен рисунок для первого примера.
Частичные правильные решения для тестов, в которых \(a_1\), \(a_2\), \(a_3\), \(a_4\) ≤ \(10^5\), будут оцениваться из 50 баллов.
2 2 2 2
2
При регистрации на портале интернет-олимпиады все участники заполняют регистрационную форму, где они указывают название школы, в которой они учатся. Разные участники могут по-разному писать название школы, например, «Физико-математическая школа №18», «ФМШ №18».
Организаторам олимпиады предоставлена информация о названиях школ, которые написали регистрируемые участники олимпиады. Точно известно, что цифры в названии школы встречаются только в номере школы, а число в записи названия школы встречается ровно один раз и оно однозначно определяет номер школы. Номер школы является положительным целым числом и не может начинаться с нуля.
Требуется написать программу для сайта интернет-олимпиады, которая поможет организаторам олимпиады получить следующую информацию: количество школ и номера школ, из которых зарегистрировалось не более пяти участников.
Первая строка входного файла содержит одно целое число n (1 ≤ \(n\) ≤ 1000) – количество названий школ, указанных всеми участниками при регистрации.
Последующие \(n\) строк содержат названия школ, указанные всеми участниками. Название школы содержит только заглавные и строчные буквы латинского алфавита, цифры и пробелы, длина названия не превышает 100 символов.
Первая строка выходного файла должна содержать одно число \(m\) – количество школ, от которых на олимпиаду зарегистрировалось от одного до пяти участников. Последующие \(m\) строк должны содержать только номера таких школ, при этом номера должны располагаться по одному в строке в произвольном порядке.
В приведенном примере для участия в интернет-олимпиаде зарегистрировались: два ученика из школы с номером 18, один ученик из школы с номером 42 и шесть учеников из школы с номером 9. Таким образом, от 1 до 5 участников зарегистрировано от школ с номерами 18 и 42.
Частичные правильные решения для тестов, в которых все номера школ являются однозначными числами, будут оцениваться из 30 баллов.
Частичные правильные решения для тестов, в которых номера школ – это числа строго меньше 1000, будут оцениваться из 50 баллов.
Частичные правильные решения для тестов, в которых номера школ – это числа строго меньше 109, будут оцениваться из 80 баллов.
Несмотря на выделение отдельных групп тестов, на окончательную проверку будут приниматься только решения, правильно работающие для теста из условия задачи.
9 Physics and Mathematics School 18 9ya shkola imeni Pushkina Lyceum 9 PaMS 18 Gymnasium 42 School 9 Shkola nomer 9 High school 9 School N 9
2 18 42
На межрегиональной олимпиаде по программированию роботов соревнования проводятся в один тур и в необычном формате. Задачи участникам раздаются последовательно, а не все в самом начале тура, и каждая \(i\)-я задача (1 ≤ \(i\) ≤ \(n\)) становится доступной участникам в свой момент времени \(s_i\). При поступлении очередной задачи каждый участник должен сразу определить, будет он ее решать или нет. В случае, если он выбирает для решения эту задачу, то у него есть \(t_i\) минут на то, чтобы сдать ее решение на проверку, причем в течение этого времени он не может переключиться на решение другой задачи. Если же участник отказывается от решения этой задачи, то в будущем он не может к ней вернуться. В тот момент, когда закончилось время, отведенное на задачу, которую решает участник, он может начать решать другую задачу, ставшую доступной в этот же момент, если такая задача есть, или ждать появления другой задачи. При этом за правильное решение \(i\)-й задачи участник получает \(c_i\) баллов.
Артур, представляющий на межрегиональной олимпиаде один из региональных центров искусственного интеллекта, понимает, что важную роль на такой олимпиаде играет не только умение решать задачи, но и правильный стратегический расчет того, какие задачи надо решать, а какие пропустить. Ему, как и всем участникам, до начала тура известно, в какой момент времени каждая задача станет доступной, сколько времени будет отведено на ее решение и сколько баллов можно получить за ее решение. Артур является талантливым школьником и поэтому сможет успешно решить за отведенное время и сдать на проверку любую задачу, которую он выберет для решения на олимпиаде.
Требуется написать программу, которая определяет, какое максимальное количество баллов Артур сможет получить при оптимальном выборе задач, которые он будет решать, а также количество и перечень таких задач.
Первая строка входного файла содержит одно целое число \(n\) (1 ≤ \(n\) ≤ \(10^5\)) количество задач на олимпиаде.
Последующие \(n\) строк содержат описания задач, по три числа на каждой строке: \(s_i\) момент появления \(i\)-й задачи в минутах, \(t_i\) время, отведенное на ее решение в минутах, и \(c_i\) сколько баллов получит участник за решение этой задачи (1 ≤ \(s_i\), \(t_i\), \(c_i\) ≤ \(10^9\)).
Первая строка выходного файл должна содержать одно число – максимальное количество баллов, которое сможет получить Артур на олимпиаде.
Вторая строка должна содержать одно целое число \(m\) - количество задач, которые надо решить при оптимальном выборе.
Третья строка должна содержать \(m\) разделенных пробелом целых чисел - номера этих задач в порядке их решения. Задачи пронумерованы, начиная с единицы, в порядке их описания во входном файле.
Если оптимальных ответов несколько, необходимо вывести любой из них.
В первом примере Артур успевает решить все задачи и получить три балла.
Во втором примере Артуру выгоднее решать последнюю задачу и получить за нее три балла, чем решать только первые две и получить два балла.
Частичные правильные решения для тестов, в которых все \(c_i\) одинаковы и \(n\) ≤ 1000, оцениваются из 30 баллов.
Частичные правильные решения для тестов, в которых все \(c_i\) одинаковы, оцениваются из 50 баллов.
Частичные правильные решения для тестов, в которых \(n\) ≤ 1000, оцениваются из 50 баллов.
2 1 1 1 2 2 2
3 2 1 2
3 1 2 1 3 2 1 2 4 3
3 1 3