Задача №111586. Факториальная система счисления

В факториальной системе счисления основаниями являются последовательность факториалов b_k = k!, и каждое натуральное число x представляется в виде:

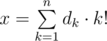$\text{[math]}$ , где 0 ≤ d_k ≤ k

Ваша задача определить по данному в факториальной системе счисления числу его остаток от деления на p.

Входные данные

В первой строке даны два натуральных числа n и p, где n - максимальный индекс такой, что d_n ≠ 0 (1 ≤ n ≤ 200, 2 ≤ p ≤ 10⁴). Во второй строке задана последовательность d_n, ..., d₁, корректно определяющая некоторое натуральное число x.

Выходные данные

Выведите одно число — остаток от деления x на p.

Примеры тестов

Входные данные

5 6
1 3 3 2 1

Выходные данные

Примечание

В исходном примере x = 215

Сдать: для сдачи задач необходимо войти в систему