Задача №111592. Бесконечная периодическая дробь
Известно, что запись числа A в позиционных системах счисления с основанием p и q имеет вид бесконечной периодической дроби с периодом 2:
Написать программу, которая для введенных натуральных чисел p и q находит и выводит все возможные пары значений цифр a и b, удовлетворяющих соотношению ( * ).
Входные данные
Даны два числа p и q (2 ≤ p < q ≤ 105).
Выходные данные
В первой строке выведите число k — количество пар a и b. Далее в n строках выведите эти пары (a < b). Пары следует выводить в порядке возрастания a, а если они равны, то в порядке возрастания b. Если пар нет, то k должно быть равно 0.
Примеры тестов
Входные данные
5 11
Выходные данные
1
1 4
Примечание
Значением числа, запись которого в позиционной системе счисления с основанием s есть 0, cdef (где c, d, e, f - цифры), является 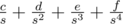
Сдать: для сдачи задач необходимо войти в систему