Задача №111653. Открытие

Прямо с вокзала Егор и Саша отправились на открытие ВКОШП. Так как они прибыли позже всех, то им достались места в последнем ряду.

Вдруг друзья заметили, что все участники, которые сидят перед ними, рассматривают на своих ноутбуках Pinebook разные фрагменты одной большой картинки. Друзьям стало интересно, что это за картинка. К счастью, Егор совершенно случайно взял с собой пульт PineappleRemote, с помощью которого можно обменять фрагменты картинки между двумя любыми компьютерами. Естественно, при этом могут возмущаться владельцы этих компьютеров, поэтому Саша и Егор хотят, чтобы количество обменов не превышало пяти миллионов.

Перед ними расположены n рядов по m мест, на каждом из которых есть ноутбук с фрагментом картинки. Саша поставил в соответствие каждому фрагменту номер таким образом, что:

  • все номера различны;
  • если расставить все фрагменты в порядке возрастания номеров в n рядов по m штук, то получится целостная картинка.

Но, к сожалению, праздничная церемония, оригинальная музыка и блестящие ведущие так понравились друзьям, что они подумали: "Кто, если не Вы сможете составить список действий, после которых на Pinebook-ах они смогут увидеть картинку целиком?".

Входные данные

В первой строке находятся два натуральных числа n и m — количество рядов и количество мест в каждом из них. Далее идут n строк по m чисел в каждом: j-ое число на i-ой строке является номером фрагмента на ноутбуке, стоящем на j-ом месте i-ого ряда.

Выходные данные

В первой строке выведите число c (0 ≤ c ≤ 5000000) — количество обменов фрагментов изображения между ноутбуками, которые необходимо произвести. Следующие c строк должны содержать информацию о совершенных обменах. В i строке выведите четыре натуральных числа: x1, y1, x2, y2 (1 ≤ x1, x2 ≤ n;1 ≤ y1, y2 ≤ m) — номера рядов и мест компьютеров, между которыми происходит i-ый по счету обмен. Вывод двух одинаковых позиций (x1 = x2 и y1 = y2) будет расцениваться как неправильный ответ!

Если существует несколько правильных ответов, выведите любой из них.

Примечание

Пояснение к первому тесту: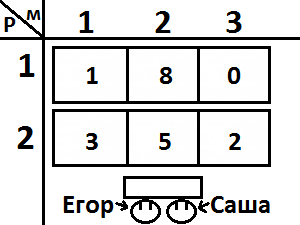

Тесты в этой задаче состоят из пяти групп:

  1. Тесты 1-2. Тесты из условия. Оцениваются в 0 баллов.
  2. Тесты 3-12. Тесты с ограничением 1 ≤ NxM ≤ 100; |aij| ≤ 1000. Группа тестов оценивается в 25 баллов, при этом баллы ставятся только за прохождение всех тестов группы.
  3. Тесты 13-22. Тесты с ограничением 1 ≤ NxM ≤ 1000; |aij| ≤ 10000. Группа тестов оценивается в 25 баллов, при этом баллы ставятся только за прохождение всех тестов 1 и 2 группы.
  4. Тесты 23-37. Тесты с ограничением 1 ≤ NxM ≤ 105; |aij| ≤ 109. Группа тестов оценивается в 25 баллов, при этом баллы ставятся только за прохождение всех тестов 1, 2 и 3 группы.
  5. Тесты 38-52. Тесты с ограничением 1 ≤ NxM ≤ 105; |aij| ≤ 1018. Группа тестов оценивается в 25 баллов, при этом баллы ставятся только за прохождение всех тестов 1, 2, 3 и 4 группы.

Примеры
Входные данные
2 3
1 8 0
3 5 2
Выходные данные
3
1 1 1 3 
1 2 2 3 
1 2 1 3
Входные данные
1 1
42
Выходные данные
0
Сдать: для сдачи задач необходимо войти в систему