Что может быть проще простого числа? Казалось бы, объяснить, что такое простое число, можно даже человеку, совершенно далёкому от математики: целое число называется простым, если оно не меньше двух и не делится ни на какое целое положительное число, кроме единицы и самого себя. Это определение будет понятно даже третьекласснику, только-только познакомившемуся с делением. Что может быть проще? Но, как часто случается в математике, за кажущейся простотой определения скрывается очень глубокая теория с множеством нетривиальных фактов, многие из которых остаются недоказанными и по сей день.

Прочитав популярную книгу Д. Дербишира «Простая одержимость» , Леопольд узнал следующий занятный факт. Оказывается, существует Теорема о распределении простых чисел , гласящая, что количество простых чисел, не превышающих N , можно очень точно оценить как 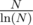. Например, начиная с N > 5000 , эта формула даёт ошибку, не более чем в 15% от реального значения. Более того, с ростом N относительная погрешность такой оценки падает, стремясь к нулю.

Леопольд крайне заинтересовался простыми числами и связанной с ними теорией. Он решил выдвинуть какую-нибудь не менее важную и серьёзную гипотезу, а потом доказать её, и назвать полученный факт теоремой Леопольда. Для этого ему нужна помощь в отыскании закономерностей, описывающих простые числа. Он просит вас написать для него программу, которая ищет для него Q отрезков, i -й из которых состоит из L _i последовательных натуральных чисел и содержит определённое количество K _i простых чисел. Для простоты анализа он просит вас ограничиться в поисках первыми десятью миллионами чисел. Помогите ему, и, возможно, вам с ним удастся оставить след в истории!