Задача №112574. Тяжёлый валун
Флатландский валун имеет форму многоугольника (не обязатеьно выпуклого). Для простоты будем рассматривать только многоугольники, у которых любые 3 вершины не лежат на одной прямой. Такие валуны получаются из разных видов камней, необязательно однородной плотности. Тем не менее, вы знаете расположение его центра тяжести.
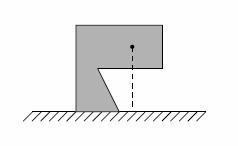 Сейчас мы положили на горизонтальную прямую две вершины камня (назовём их базовыми), и отпустили. В случае, если центр тяжести находится над отрезком, соединяющим базовые вершины, или над базовыми вершинами, то валун будет стоять. Иначе сила тяжести заставит его катится в определённом направлении.
Сейчас мы положили на горизонтальную прямую две вершины камня (назовём их базовыми), и отпустили. В случае, если центр тяжести находится над отрезком, соединяющим базовые вершины, или над базовыми вершинами, то валун будет стоять. Иначе сила тяжести заставит его катится в определённом направлении.
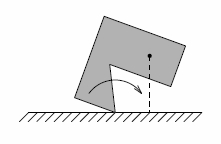
Валун будет перемещаться на одной из базовых вершин, пока он не коснётся горизонтальной прямой другой вершиной. Будем называть этот процесс поворотом. Теперь одна из базовых вершин поменялась, и возможно центр тяжести теперь находится над отрезком, соединяющим базовые вершины. В этом случае валун остановится.
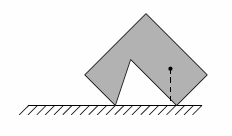
Иначе он продолжит вращаться, пока в конце концов не остановится, так как во Флатляндии вечный двигатель невозможен. Движение валуна происходит в вязкой среде, то есть инерция отсутствует, и валун остановится, как только сила тяжести позволит ему. Зная координаты вершин валуна и его центра тяжести, вычислите количество поворотов, которые совершит валун перед остановкой.
Входной файл содержит целое число N (3 ≤ N ≤ 100) . В следующих N + 1 строках находятся пары целых чисел. Первые N пар описывают координаты вершин валуна, перечисленные в порядке обхода по или против часовой стрелки (линия, на которой стоит валун, описывается уравнением y = 0 ; гравитация действует параллельно Oy в стороны отрицательных y ). Последняя пара чисел описывает центр тяжести. Все координаты — целые числа, не превосходящие по абсолютному значению 30 000 , все y -координаты — неотрицательные. Никакие 3 вершины не лежат на одной прямой. Центр тяжести находится внутри валуна.
Выведите одно число — количество поворотов