Задача №113169. Дождик
В НИИ метеорологии решили изучить процесс образования водоемов на различных рельефах местности во время дождя. Ввиду сложности реальной задачи была создана двумерная модель, в которой местность имеет только два измерения — высоту и длину. В этой модели рельеф местности можно представить как N-звенную ломаную c вершинами \((x_0, y_0), ..., (x_N, y_N)\), где \(x_0 < x_1 < ... < x_N\) и \(y_i \neq y_j\), для любых \(i \neq j\). Слева в точке \(x_0\) и справа в точке \(x_N\) рельеф ограничен вертикальными горами огромной высоты.
Если бы рельеф был горизонтальным, то после дождя вся местность покрылась бы слоем воды глубины H. Но поскольку рельеф — это ломаная, то вода стекает и скапливается в углублениях, образуя водоемы.
Требуется найти максимальную глубину в образовавшихся после дождя водоемах.
В первой строке расположены натуральное число \(N (1 \le N \le 100)\) и \(H\) — действительное число, заданное с тремя цифрами после десятичной точки \((0 \le H \le 10^9)\). В последующих \(N + 1\) строках — по два целых числа \(x_i, y_i: -10000 \le x_i, y_i \le 10000 (0 \le i \le N)\).
Числа в строках разделены пробелами.
Ответ должен содержать единственное число — искомую глубину с точностью до 4-х знаков после десятичной точки.
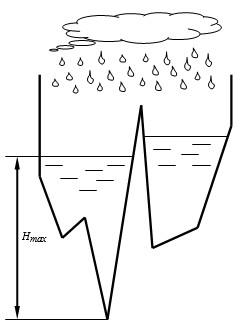
7 7.000 -5 10 -3 4 -1 6 1 -4 4 17 5 3 9 5 12 15
15.8446