Задача №113359. Медианное сглаживание
Школьник Вася очень любит читать книжки по программированию и математике. Недавно он прочёл в энциклопедии статью, в которой рассказывалось о методе медианного сглаживания и его многочисленных применениях в науке и технике. Идея метода Васе очень понравилась, и он решил опробовать его на практике.
При использовании простейшего варианта медианного сглаживания по последовательности чисел a 1 , a 2 , ..., a n строится новая последовательность чисел b 1 , b 2 , ..., b n по следующему алгоритму:
- b 1 = a 1 , b n = a n , то есть первое и последнее число новой последовательности совпадают с соответствующими числами исходной последовательности.
- При i = 2, ..., n - 1 значение b i полагается равным медиане трёх значений a i - 1 , a i и a i + 1 .
Напомним, что медианой набора из трех чисел называется число, которое окажется на втором месте, если три числа выписать в порядке неубывания. Например, медианой набора 5, 1, 2 является число 2, а медианой набора 1, 0, 1 — число 1.
Чтобы не усложнять себе задачу, Вася решил применять метод только к последовательностям, состоящим из нулей и единиц.
Проделав нехитрую процедуру один раз, Вася посмотрел на получившуюся последовательность и подумал: что будет, если снова применить к ней алгоритм, а потом применить его к следующему результату и так далее? Рассмотрев пару примеров, Вася обнаружил, что через несколько применений медианного сглаживания последовательность может перестать изменяться. Будем говорить, что последовательность стабильна , если она не изменяется при применении к ней медианного сглаживания.
Васе стало интересно, всегда ли последовательность рано или поздно становится стабильной. Он просит вас написать программу, которая по заданной последовательности нулей и единиц определит, становится ли она когда-нибудь стабильной, и если да, то сколько раз для этого нужно применить к ней метод медианного сглаживания.
В первой строке входных данных находится одно целое число n ( 3 ≤ n ≤ 500 000 ) — число элементов в рассматриваемой последовательности.
В следующей строке находится исходная последовательность чисел a 1 , a 2 , ..., a n , состоящая только из нулей и единиц.
В случае, если последовательность никогда не станет стабильной, выведите одно число - 1 .
В противном случае в первой строке выведите одно число — минимальное число раз, которое нужно применить алгоритм медианного сглаживания, прежде чем последовательность станет стабильной. Во второй строке выведите n чисел через пробел — саму итоговую последовательность.
Во втором примере стабилизация наступает через два шага:
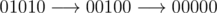 , а последовательность
00000
, как нетрудно заметить, является стабильной.
, а последовательность
00000
, как нетрудно заметить, является стабильной.
4 0 0 1 1
0 0 0 1 1
5 0 1 0 1 0
2 0 0 0 0 0