Задача №113948. LinkedList's Bizarre Adventure
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
В первой строке содержится одно целое число \(n\) (\(1 \leq n \leq 300\,000\)) — число сообщений в примере тимлида. Следующие \(n - 1\) строк задают связи между сообщениями. Каждая из них содержит два целых числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\), \(a_i \neq b_i\)), которые показывают, что сообщения с номерами \(a_i\) и \(b_i\) связаны.
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
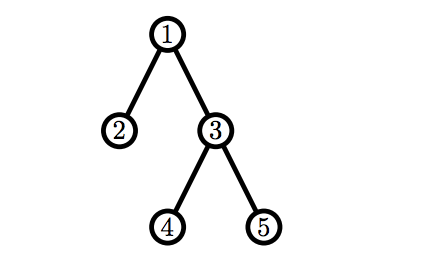
В первом примере Билли первым ходом может удалить одну из вершин с номерами \(2\), \(4\) или \(5\), так как они являются листьями. Он не будет удалять вершину с номером \(4\) или \(5\), так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину \(2\). В свою очередь, Рикардо может удалить вершины \(1\), \(4\) или \(5\), и, в любом случае, Билли получит от него корректный граф.
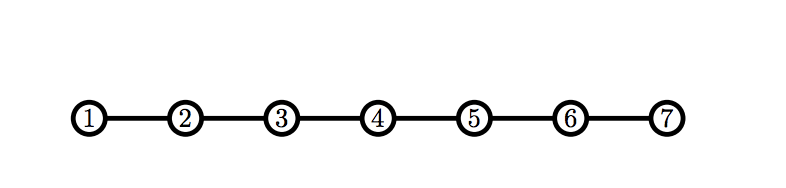
Во втором примере у Билли сразу есть корректный граф.
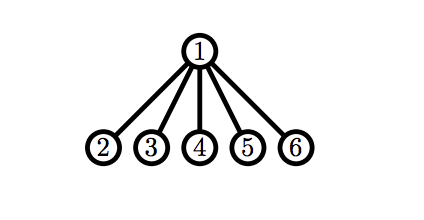
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
5 1 2 1 3 3 4 3 5
Billy
7 1 2 2 3 3 4 4 5 5 6 6 7
Billy
6 1 2 1 3 1 4 1 5 1 6
Ricardo