Задача №114330. Адриатика
Будем считать, что карта Адриатического моря представляет собой сетку, состоящую из единичных квадратиков, организованных в \(2500\) рядов и \(2500\) столбцов. Ряды пронумерованы от \(1\) до \(2500\) с севера на юг, столбцы пронумерованы от \(1\) до \(2500\) с запада на восток. В море есть N островов, пронумерованных от 1 до N и каждый остров находится внутри некоторого единичного квадрата сетки. Позиция острова K задана его координатами — рядом \(R_k\) и столбцом \(C_k\). Никакие два острова не находятся в одном квадрате.
Из за ветра и морских течений, за один шаг переплыть с одного острова на другой можно только, если они расположены в северо-западном или юго-восточном направлении друг относительно друга.
Точнее, можно переплыть с острова \(A\) на остров \(B\) за один шах, если или \(R_A \lt R_B\) и \(C_A \lt C_B\), или \(R_A \gt R_B\) и \(C_A \gt C_B\). При этом расстояние между островами или наличие островов по дороге не влияет на возможность доплыть с одного острова на другой. Если нельзя доплыть с одного острова на другой напрямую, иногда можно доплыть с использованием промежуточных островов более чем за один шаг. Определим как расстояние между островами величину, равную числу шагов, необходимых, чтобы переплыть с одного острова на другой.
Рассмотрим остров K. Для каждого острова определим, какое минимальное число шагов можно переплыть с него на K. Просуммируем эти числа и получим некоторую величину, характеризующую удаленность K от остальных островов. Требуется найти это число для всех островов. Гарантируется, что в тестах острова расположены так, что с каждого острова можно попасть на каждый.
Первая строка входного файла содержит целое число \(n\) (\(3 \le n \le 250000\)) – число островов.
Следующие \(n\) строк сожержат положения островов. Каждое положение задаётся двумя целыми числами \(r_i\) и \(c_i\) между 1 и 2500 (включительно) - ряд и столбец, сооответственно.
Выходной файл должен содержать \(n\) строк. Для каждого острова, в порядке вхождения во входно файле, выведите на отдельной строке сумму расстояний дл него со всех остальных островов.
Подзадача 1 (25 баллов): \(1 \le n \le 100\)
Подзадача 2 (25 баллов): \(1 \le n \le 1500\)
Подзадача 3 (10 баллов): \(1 \le n \le 5000\)
Подзадача 4 (20 баллов): \(1 \le n \le 25000\)
Подзадача 5 (20 баллов): Без дополнительных ограничений
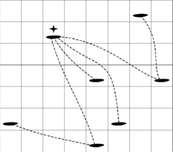
Пояснение к первому примеру:
На рисунке можно, начав с острова в ряду 2, столбце 3, можно доплыть за один шаг до 4 других островов, а до оставшихся двух островов - за 2 шага.
7 1 7 7 5 4 5 4 8 6 6 6 1 2 3
16 11 12 11 12 16 8
4 1 1 2 3 3 2 4 4
3 4 4 3