Теоретический материал

Числа Каталана

Рассмотрим произвольное арифметическое выражение. Теперь сотрем в этом выражении всё кроме скобок. Получившуюся последовательность из скобок будем называть «правильной скобочной последовательностью». Любая правильная скобочная последовательность состоит из равного числа открывающихся и закрывающихся скобок. Но этого условия недостаточно: например, скобочная последовательность «(())» является правильной, а последовательность «)()(» -- нет.

Можно дать и точное определение правильной скобочной последовательности.

  1. Пустая последовательность (то есть не содержащая ни одной скобки) является правильной скобочной последовательностью.
  2. Если «A» -- правильная скобочная последовательность, то «(A)» (последовательность A, взятая в скобки) -- правильная скобочная последовательность.
  3. Если «A» и «B» -- правильные скобочные последовательности, то «AB» (подряд записанные последовательности A и B) -- правильная скобочная последовательность.

Обозначим количество правильных скобочных последовательностей длины 2n (то есть содержащих n открывающихся и n закрывающихся скобок) через Cn и решим задачу нахождения Cn по заданной величине n.

Для небольших n значения Cn несложно вычислить полным перебором. C0 = 1 (правильная скобочная последовательность длины 0 ровно одна -- пустая), C1 = 1 (последовательность «()»), C2 = 2 (последовательности «(())» и «()()»), C3 = 5 («((()))», «(()())», «(())()», «()(())», «()()()»).

Запишем рекуррентную формулу для Cn. Пусть X -- произвольная правильная скобочная последовательность длины 2n. Она начинается с открывающейся скобки. Найдем парную ей закрывающуюся скобку и представим последовательность X в виде:

X = (A)B,

где A и B -- тоже правильные скобочные последовательности. Если длина последовательности A равна 2k, то последовательность A можно составить Ck способами. Тогда длина последовательности B равна 2(n - k - 1) и последовательность B можно составить Cn - k - 1 способами. Комбинация любого способа составить последовательность A с любым способом составить последовательность B даст новую последовательность X, а величина k может меняться от 0 до n - 1. Получили рекуррентное соотношение:

Cn = C0Cn - 1 + C1Cn - 2 + C2Cn - 3 +...+ Cn - 2C1 + Cn - 1C0.

Напишем функцию, вычисляющую значение Cn по данному n: 

int Catalan(int n) 
{ 
  int C[n+1]; 
// Создаем массив для хранения C[m] 
  C[0]=1; 
  for (int m=1; m<=n; ++m)   // Вычисляем C[m] для m=1..n 
  { 
    C[m]=0; 
    for (int k=0; k<m; ++k) 
      C[m]+=C[k]*C[m-1-k]; 
  } 
  return C[n]; 
}

Мы назвали функцию Catalan, поскольку значения Cn называются числами Каталана в честь бельгийского математика XIX века Евгения Шарля Каталана. Начало ряда чисел Каталана выглядит следующим образом:

n 0 1 2 3 4 5 6 7 8 9 10
Cn 1 1 2 5 14 42 132 429 1430 4862 16796

Для чисел Каталана хорошо известна и нерекуррентная формула:

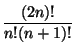Cn = $\displaystyle {C_{2n}^n\over n+1}$ = $\displaystyle {(2n)!\over n!(n+1)!}$.

Более подробно про правильные скобочные последовательности а также элементарное доказательство данной формулы можно прочесть в [1, 2.6-7].