Игра "Ним"
Для этой игры используется несколько кучек камней. За один ход разрешается взять любое количество камней из одной любой кучки (можно взять даже все камни из одной кучки). Выигрывает игрок, взявший последний камень.
Вот пример игры:
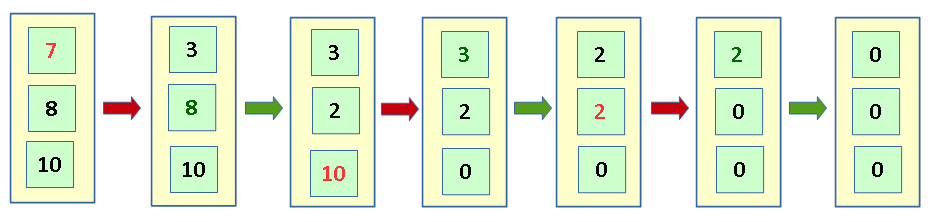
Красным цветом показан ход первого игрока, зеленым - второго.
В этой партии победил второй игрок.
Рассмотрим короткий и эффективный способ определения исхода игры в "Ним" (при условии, что оба игрока играют разумно).
Пусть для игры взяли кучки из 7, 8 и 10. Разложим эти числа в суммы степеней двоек, как показано в таблице:
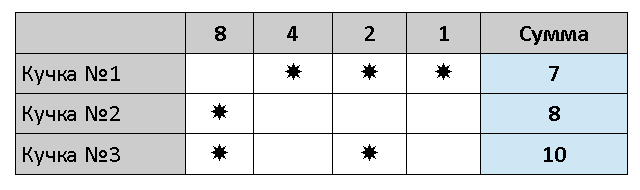
Первый игрок должен сделать такой ход, чтобы в каждом столбце осталось четное число звездочек. Для этого он может взять 5 камней из первой кучки, оставив сопернику такую позицию:
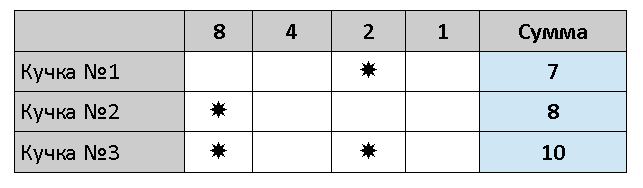
Теперь второй игрок вынужден нарушить четность количества звездочек хотя бы в одном из столбцов: ведь он может брать камни только из одной кучки, то есть менять только одну из строк таблицы. Предположим, что он взял 3 камня из последней кучки, оставив первому такую позицию:

Первый игрок снова может восстановить четность во всех столбцах, взяв три камня из второй кучки:
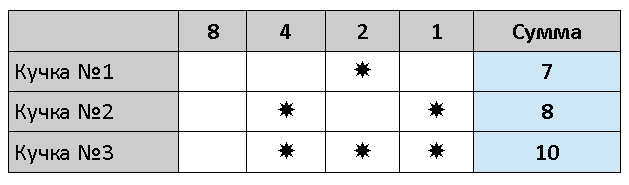
Так игра продолжается до тех пор, пока первый игрок не заберет последний камень.
Позиция является выигрышной тогда и только тогда, когда количество звездочек в каждом столбце четно. В противном случае позиция является проигрышной. Это правило верно для любого количества кучек камней, в этом случае порязрядный XOR нужно применить ко всем числам.
Сформулируем полученный результат более формально.
Пусть m и n — неотрицательные целые числа.
Возьмем двоичные представления этих чисел, и применим к ним поразрядно операцию "исключающее или" (XOR).
Позиция (m, n) является проигрышной тогда и только тогда, когда m XOR n = 0.
Рассмотрим пример. Пусть m = 21 и n = 39, переведем эти числа в двоичную систему и вычислим поразрядный XOR:
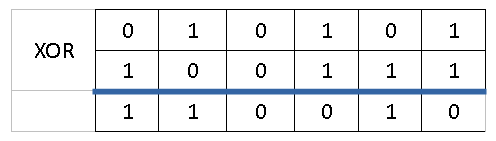
Таким образом, комбинация камней 21 и 39 является выигрышной.
Выигрышные ходы
Итак мы выяснили, что игрок, который каждым своим ходом восстанавливает четность количества камней во всех кучках, выигрывает. Но почему из любой позиции можно получить позицию с четным числом камней во всех кучках? Для этого можно воспользоваться следующим алгоритмом нахождения выигрышного хода.
Мы будем иллюстрировать шаги нашего алгоритма на примере позиции (19, 25, 12)
Представим числа в двоичной системе и применим поразрядно операцию XOR.
Найдем самую левую ненулевую цифру суммы, и мысленно сотрем все, что записано левее. В нашем примере это будет выглядеть так:
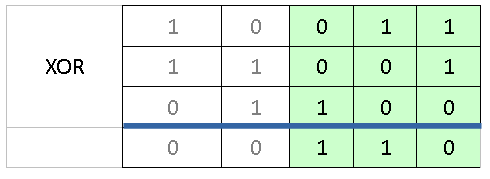
Действительно, цифры левее найденной уже равны 0 и делать с ними еще что-то не нужно, наоборот, вмешательство требуется в правой части, где в результате получаются единицы в разных разрядах.
Среди оставшихся слагаемых выберем наибольшее. В нашем примере это число 01100.
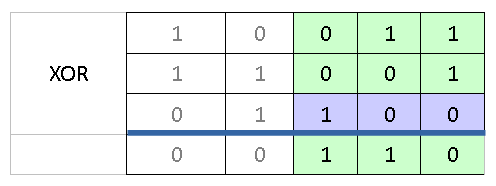
Уменьшим это слагаемое до требуемого значения.Чтобы получить результат (00000), необходимо уменьшить выбранное число до (01010).
Примеры других игр.
В шоколадке размером m x n долек в одной из долек оказался камень. Двое играют в такую игру: они по очереди разламывают шоколадку на две части по одной из линий, и съедают часть без камня. Проигрывает тот, кому достается одна долька с камнем. Кто выигрывает при правильной игре?
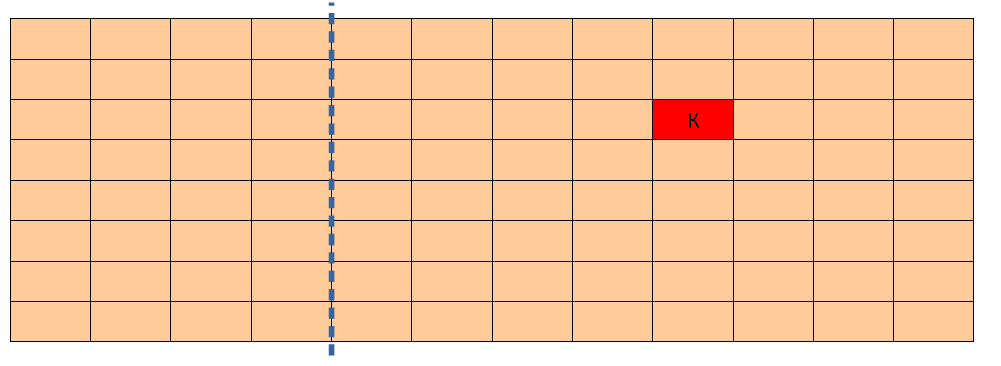
На полоске 1 x n в каждой клетке может лежать не более одной монеты. За один ход разрешается передвинуть любую монету влево на любое количество клеток не перепрыгивая через другие монеты. Проигрывает игрок, который не может сделать очередного хода.

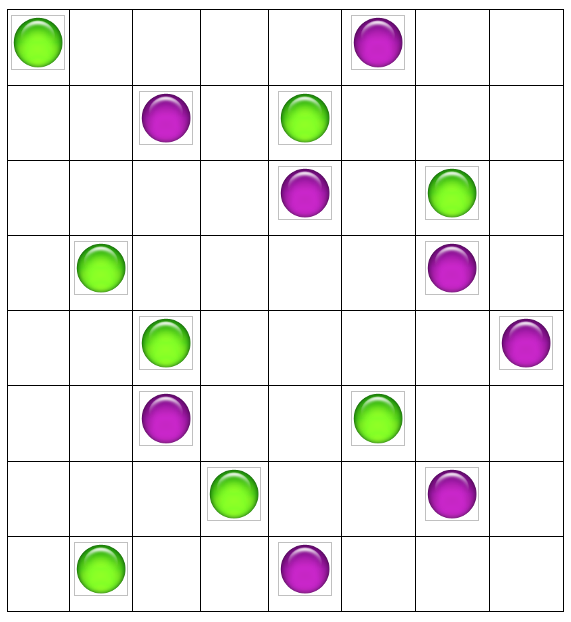
В следующей игре каждый из игроков контролирует фишки одного цвета. За один ход можно передвинуть любую фишку своего цвета на любое количество клеток влево или вправо, не перепрыгивая через другие фишки. Кто выигрывает при правильной игре? Может ли эта игра закончится вничью при правильной игре обоих игроков?
Изменим правила игры Ним: будем считать проигравшим того игрока, который возьмет последний камень. Как изменится анализ этой игры?