Рассмотрим игру "Фишка на графе", но в этот раз разрешим наличие циклов в графе.
Правила игры. Дан ориентированный граф, в одной из вершин которого находится фишка. Играют двое, ходы делаются по очереди. Игрок своим ходом может переместить фишку из текущей вершины в любую, куда существует ребро. Проигрывает тот, кто не может сделать следующий ход.
Как и в предыдущих примерах этого курса можно установить, что вершины, не имеющие исходящих ребер являются проигрышными, но с определением статуса остальных вершин возможны осложнения из-за появления циклов.
Рассмотрим пример. Пусть дан граф:
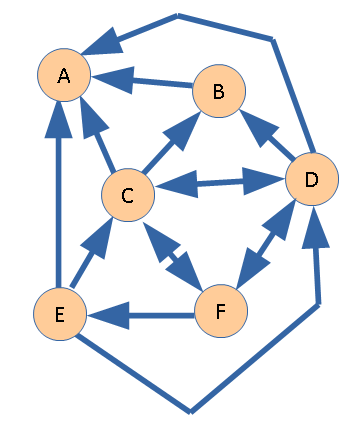
Попытаемся построить функцию Шпрага-Гранди для всех вершин графа.
Вершина A является проигрышной, так как у нее отсутствуют исходящие ребра.
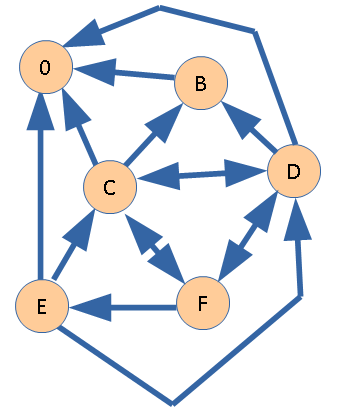
Вершина B имеет единственное исходящее ребро, ведущее в вершину A, поэтому вершине B будет соответствовать значение функции F(B) = 1.
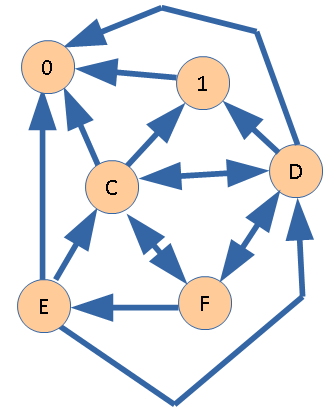
Далее применение обычного правила становится затруднительным из-за наличия циклов. Поэтому, его необходимо расширить.
Во-первых, пометим те вершины, значения функции для которых мы уже вычислили.
Во-вторых, для каждой следующей вершины V будем применять такое правило:
- Рассмотрим все помеченные вершины, в которые есть ребра из V. Найдем наименьшее неотрицательное число, которого нет среди значений функции для этих вершин. Пусть такое число нашлось, обозначим его M.
- Проверим, можем ли мы приписать рассматриваемой вершине V значение M. Для этого рассмотрим все ребра, ведущие из вершины V в неотмеченные вершины. Если для каждой из этих неотмеченных вершин существует путь в какую-то уже отмеченную вершину, у которой есть оценка F = M, то можно и "нашей" текущей вершине присвоить оценку F(V)=M.
Пример. Отметим зеленым цветом все отмеченные вершины. Рассмотрим вершину E.
У вершины E есть единственное ребро, ведущее в помеченную вершину - EA. F(A) = 0, следовательно, логично было бы приписать вершине E значение F(E)=1.
Проверим, возможно ли это. Рассмотрим ребра, ведущие из вершины E в непомеченные вершины. Таких ребра два: EC и ED. Из обеих этих вершин (C и D) есть пути в вершину B, у которой отметка F(B) = 1.
Таким образом, вершине E можно присвоить значение F(E) = 1.
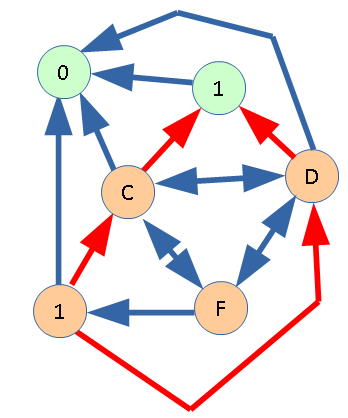
Пометим вершину E и продолжим рассуждение.
Рассмотрим вершину F. У нее есть единственное ребро, ведущее в помеченную вершину - FE, причем F(E) = 1. Логично было бы присвоить вершине F значение 0. Проверим, возможно ли это.
Рассмотрим ребра, ведущие из вершины F в неотмеченные вершины. Таких ребра два: FC и FD. Через обе вершины C и D существует путь, ведущий в вершину A, значение функции для которой равно 0.
Вывод. Можно присвоить вершине F значение F(F) = 0.
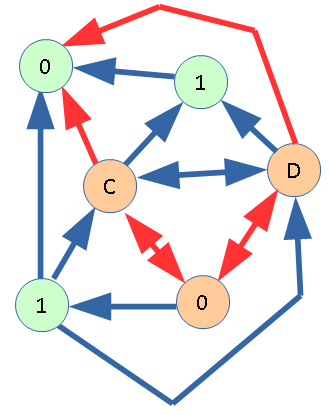
Также пометим вершину F и продолжим рассуждение.
Рассмотрим вершину C. Из нее есть 4 ребра, ведущие в отмеченные вершины. Значения функции в этих вершинах равны 0 и 1. Следующее число, которое мы могли бы взять в качестве значения функции равно 2. Проверим, возможно ли это.
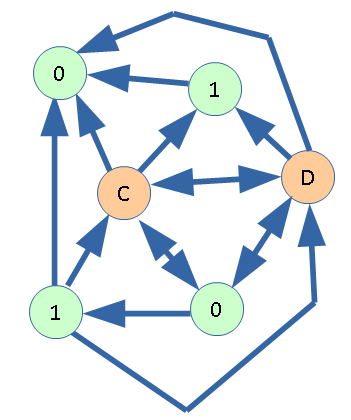
Из вершины C выходит единственное ребро, ведущее в неотмеченную вершину D. Из вершины D нет пути, ведущего в какую-либо вершину со значением функции равным 2.
Вывод: для вершины C (аналогично, для вершины D) нельзя взять значение функции равное 2. Вместо этого будем использовать значение функции, равное бесконечности.
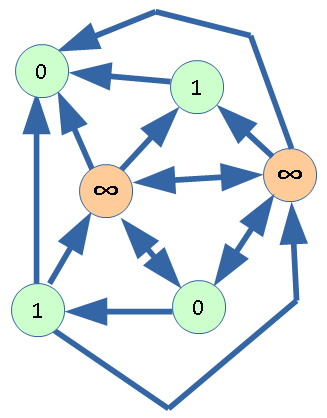
Перейдем теперь к применению полученных значений для выбора выигрышных ходов.
Сформулируем утверждения в общем случае. Пусть в вершинах графа расставлены несколько фишек. В таком случае, возможны следующие варианты:
- Значения функции во всех вершинах, где расположены фишки, являются конечными. В этом случае исход игры и выбор хода определяется также, как и в случае когда циклы отсутствуют.
- Среди вершин, в которых стоят фишки, имеется ровно одна с бесконечным значением. В этом случае возможны два варианта:
- Если из вершины с бесконечным значением существует ход в вершину с конечным значением, который переводит позицию в проигрышную, то это выигрышная позиция (игра этим ходом сводится к предыдущему пункту, сопернику достается проигрышная позиция)
- В противном случае результатом будет ничья (можно сделать такой первый ход, что после него игра будет продолжаться сколь угодно долго)
- Если есть хотя бы 2 вершины с бесконечным значением функции, то игра закончится вничью (оба игрока могут сколь угодно долго препятствовать другому выиграть).