Пример реализации
Пусть целевая функция F(x, y) задана формулой:
F(x, y) = x4 + 8x3 - 20x2 + (6y - 4)4
На рисунке показана поверхность, соответствующая данной формуле.
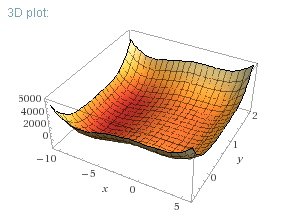
Примечание. Разумеется, поскольку выражение достаточно "хорошее" в математическом плане, то эту задачу не обязательно решать с помощью генетического алгоритма, здесь можно применить, например, методы покоординатного или градиентного спуска, или заняться предварительным математическим исследованием функции. Однако, задача данной статьи - продемонстрировать работу генетического алгоритма, и лучше это делать на примере, где читатель может сам найти правильный ответ другими методами и сравнить с тем, что получилось, при этом сравнив точность и вычислительные затраты.
Идея генетического алгоритма взята из эволюции живых организмов. Эволюция, в некотором смысле, тоже является процессом оптимизации, где целью является получение организма, наиболее приспособленного к среде обитания.
В нашей конкретной задаче есть точки с координатами (xi, yi), оптимальность которых задается целевой функцией F(x, y)
Назовем координаты точки (xi, yi) генотипом
Общая схема работы генетического алгоритма представлена на рисунке. Цикл может продолжаться:
- Исчерпания количества поколений, отпущенного на эволюцию
- Исчерпания времени, отпущенного на эволюцию
- Завершения крупных изменений в генотипе (возможное обнаружение оптимального решения);
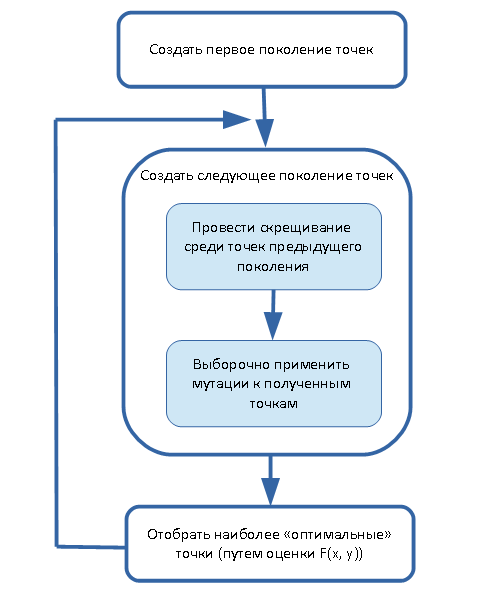
Рассмотрим более подробно разные этапы этой схемы.
В программе будут использоваться следующие описания. Пусть точка описана следующим образом:
Пусть a - массив точек.
Также будет использоваться функция make_random(), которая будет возвращать случайное число в диапазоне от -1 до 1.
Функция создания первого поколения из 10 точек будет очень простой. Создадим 10 точек с возможным координатами от -10 до +10.
Функция скрещивания двух точек и получения новой. В данном примере все точки предыдущего поколения будут допущены до формирования следующего. Существуют стратегии, когда это не так. Возьмем самый простой способ наследования: когда точка-потомок в половине случаев наследует координату x от первого родителя, а y - от второго, а в половине случаев - наоборот.
Функция не меняет первые 10 точек, так как в них записано предыдущее поколение.
Функция мутации с некоторой вероятностью (не всегда) решает, подвергнуть ли мутации конкретную точку, и если да, то какую именно координату:
Отбор наиболее оптимальных точек будет также производиться по самой простой стратегии. Вообще, таких стратегий может быть несколько. Например, по-разному может решаться вопрос: "имеют ли право точки предыдущего поколения остаться в следующем?". Подробнее о стратегиях отбора будет написано в следующей статье.
В нашем примере применим сортировку по возрастанию F(x, y). Тогда наиболее оптимальные точки займут первые 10 мест.
Основная программа может выглядеть, например, вот так:
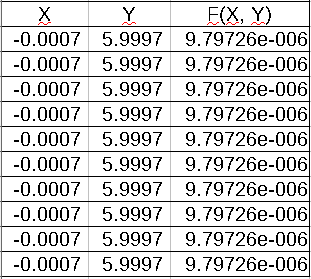
Данной программе достаточно 20 поколений точек, чтобы из сгенерированных исходных данных:
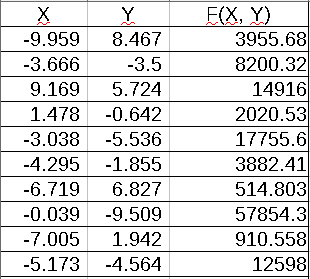
получить результаты, довольно близкие к оптимальным: