Определим множества K[i] рекуррентно. Пусть K[0] = [0, 1]. Разделим сегмент [0, 1] на три части точками и и удалим из него интервал 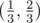. Получим множество K[1], состоящее из двух оставшихся сегментов 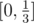и .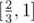

Каждый из них разделим на три части (точками и для первого сегмента, и точками и - для второго) и удалим средние интервалы 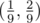и 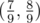. Таким образом получаем множество K[2], и т.д.

Пусть мы построим множество K[i]. Поделим каждый оставшийся сегмент из K[i] на 3 части и удалим из этих сегментов средние интервалы. Получим, таким образом, из K[i] множество K[i + 1].

Вводятся 3 целых числа n, a, b. Необходимо определить, принадлежит ли точка с координатой множеству K[n].