При проведении лотереи организаторы закладывают в лототрон n шаров с номерами от 1 до n . При процессе проведения они вынимают m 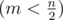шаров из лототрона совершенно случайно. У каждого участника имеется карточка, на которой выписаны p ( m ≤ p ≤ n ) различных чисел, участвующих в розыгрыше. После оглашения результатов лотереи (то есть после оглашения номеров вынутых шариков) участник вычеркивает те числа, которые есть у него и которые выпали в лотерее. Сколькими способами из скольких возможных (вывести в ответ два числа) можно угадать ровно k ( k ≤ m ) номеров?