Задача №112116. Тетрис
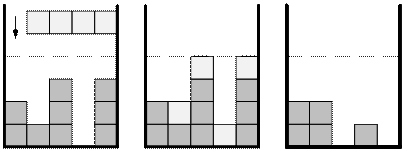
Тинки-Винки играет в модулярный тетрис. Поле состоит из N столбиков, в каждом из которых может находится от нуля до трех кубиков. После того, как в столбике оказывается четвертый кубик, все четыре кубика исчезают. За один ход игрок может выбрать произвольное количество от 1 до N последовательных столбиков, на которые упадет по одному кубику, как изображено на рисунке. Тинки-Винки хочет, начиная с имеющейся конфигурации кубиков на поле, как можно быстрее достичь определенной целевой конфигурации.
Напишите программу, которая по информации о количестве столбиков на поле, начальной и целевой конфигурации кубиков определит наименьшее количество ходов, которые должен сделать Тинки-Винки.
В первой строке входного файла содержится целое число N ( 1 ≤ N ≤ 1000 ) — количество столбиков на поле тетриса. Во сторой строке содержится N целых чисел от 0 до 3 , которые задают начальную конфигурацию кубиков на поле. В третьей строке содержится N целых чисел от 0 до 3 , которые задают конечную конфигурацию кубиков. Начальная и конечная конфигурации не совпадают.
Единственная строка выходного файла должна содержать одно целое число — минимальное возможное количество ходов Тинки-Винки для достижения целевой конфигурации.
Тесты к этой задаче состоят из пяти групп, баллы начисляются только при прохождении всех тестов группы и всех тестов некоторых предыдущих групп.
0. Тесты из условия.
1. \(N \le 10\). Эта группа оценивается в 40 баллов.
2. Нет дополнительных ограничений. Эта группа оценивается в 20 баллов.
3. \(N \le 100\). Эта группа оценивается в 25 баллов.
4. Дополнительные ограничения отсутствуют. Эта группа оценивается в 15 баллов.
5 2 1 3 0 3 2 2 0 1 0
1
4 0 1 2 3 3 2 1 0
5