Задача №112530. Многоугольник
Многоугольник состоит из всех точек, заключенных в его границах. Если для любых точек X , Y многоугольника отрезок XY лежит внутри границ, то многоугольник называется выпуклым. Все многоугольники в данной задаче выпуклы, содержат не менее двух вершин, все вершины многоугольника различные и имеют целочисленные координаты. Любая тройка вершин не коллинеарна. В дальнейшем слово многоугольник будет подразумевать все описанные выше правила.
Пусть даны два многоугольника
A
и
B
. Сумма Минковского многоугольников
A
и
B
 содержит все точки вида
(
x
a
+
x
b
,
y
a
+
y
b
)
, где
содержит все точки вида
(
x
a
+
x
b
,
y
a
+
y
b
)
, где
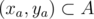 , а
, а
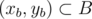 . Ясно, что сумма Минковского двух многоугольников является многоугольником.
. Ясно, что сумма Минковского двух многоугольников является многоугольником.
На картинке изображен пример суммы Минковского двух треугольников:
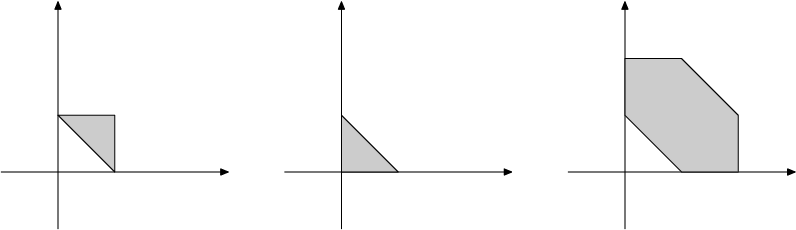
Рассмотрим операцию, обратную сумме Минковского. Пусть дан многоугольник P, мы хотим представить его в виде суммы Минковского A и B , так чтобы:
-
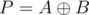 .
.
- A является либо отрезком(2 вершины), либо треугольником(3 вершины), либо четырёхугольником(4 вершины).
- A должен содержать максимально возможное число вершин.
- Если возможно A должен быть четырёхугольником, иначе если возможно A должен быть треугольником, иначе A должен быть отрезком.
Ясно, что A ≠ P и B ≠ P . Так как иначе, второе слагаемое содержало бы лишь одну вершину, что противоречит определению многоугольника.
Вам дано множество входных файлов, каждый содержит описание многоугольника P . Для каждого входного файла вы должны найти многоугольники A и B (так чтобы правила выше выполнялись) и создать выходной файл, содержащий описания многоугольников A и B . Для всех входных файлов гарантируется, что A и B существуют. Если существует несколько верных ответов, нужно выдать любой из них. Вы не должны сдавать программу, ответом являются просто выходные файлы.
Вам дан набор из 11 входных файлов с названиями 01 , 02 , ..., 11 . Каждый входной файл имеет следующий формат. Первая строка содержит одно целое число N — количество вершин многоугольника P . Следующие N строк описывают вершины многоугольника в порядке их обхода против часовой стрелки, по одной вершине в строке. Строка i + 1 содержит два целых числа x i и y i , разделённые пробелом: координаты i -й вершины многоугольника. Все координаты во входных файлах — неотрицательные целые числа.
Вы должны сдать архив их 11 выходных файлов, соответствующих данным входным файлам с описаниями искомых многоугольников A и B . Выходной файл соответствующий входному файлу с номером XX должен называться XX.out .
Формат выходного файла подобен формату входного файла. Первая строка должна содержать одно целое число N A — количество вершин многоугольника A ( 2 ≤ N A ≤ 4 ). Следующие N A строк должны описывать вершины многоугольника A в порядке обхода против часовой стрелки, по одной вершине в строке. Строка с номером i + 1 должна содержать по два целых числа x i и y i — координаты i -й вершины многоугольника A .
Числа в строке должны разделяться одним пробелом.
Строка N A + 2 должна содержать одно целое число N B — количество вершин многоугольнка B ( 2 ≤ N B ). Следующие N B строк должны описывать вершины в формате, аналогичном первому многоугольнику.
Это первый тест из выданных вам. Оба педложенных ответа на него будут правильными.